NORMSDST e NORMSINV: Calcolo distribuzioni normali

In questa sezione:

Le funzioni NORMSDST e NORMSINV eseguono calcoli sulla curva di distribuzione normale standard. NORMSDST calcola la percentuale di valori dati inferiori di o uguali al valore normalizzato; NORMSINV è l'inverso di NORMSDST, questa funzione calcola il valore normalizzato che forma il limite superiore di un percentile in una curva di distribuzione normale standard.

Inizio pagina
x
NORMSDST: Calcolo della distribuzione normale cumulativa standard

Come:

Riferimento:

La funzione NORMSDST esegue calcoli su una curva di distribuzione normale standard, calcolando la percentuale dei valori dati inferiore di o uguale al valore normalizzato. Un valore normalizzato è un punto sull'asse X di una curva di distribuzione normale standard in deviazioni standard dal significato. Questa funzione risulta utile per la determinazione di percentili in dati distribuiti normalmente.

La funzione NORMSINV è l'inverso di NORMSDST. Per informazioni su NORMSINV, consultare NORMSINV: Calcolo della distribuzione normale cumulativa inversa.

I risultati di NORMSDST sono restituiti come precisione doppia e sono 6 cifre significative.

Una curva di distribuzione normale standard è una distribuzione normale con un singificato di 0 e una deviazione standard di 1. L'area totale in questa curva è 1. Un punto sull'asse X della distribuzione normale standard è chiamato un valore normalizzato. Assumendo che i propri dati vengano distribuiti normalmente, è possibile convertire un punto dati in un valore normalizzato per trovare la percentuale di punteggio inferiore di o uguale al punteggio non elaborato.

È possibile convertire un valore (punteggio non elaborato) dai propri dati distribuiti normalmente, al valore normalizzato equivalente (punteggio-z) come segue:

z = (raw_score - mean)/standard_deviation

Per convertire da un punteggio-z ad un punteggio non elaborato, usare la seguente formula:

raw_score = z * standard_deviation + mean

Il significato di punti dati xi, dove i è 1 a n è:

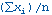
La deviazione standard di punti dati xi, dove i è 1 a n è:

Il seguente diagramma illustra i risultati delle funzioni NORMSDST e NORMSINV:
x
Riferimento: Caratteristiche della distribuzione normale

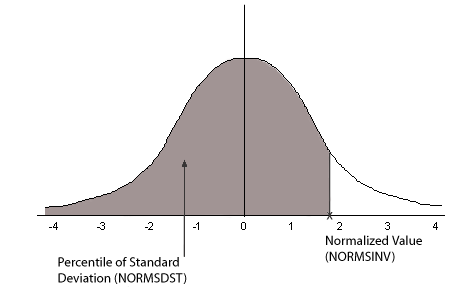
La maggior parte delle misure diffuse sono di solito distribuite. Una traccia di valori dati distribuiti normalmente approssima una curva a campana. Le due misure richieste di descrivere qualsiasi distribuzione normale sono il significato e la deviazione standard:

x
Sintassi: Come calcolare la funzione di distribuzione normale standard cumulativa
NORMSDST(value, 'D8');

dove:

valore

Valore normalizzato.

D8

Formato richiesto per il risultato. Il valore restituito dalla funzione è a precisione doppia. È possibile assegnarlo a un campo con qualsiasi formato numerico valido.
Esempio: Uso della funzione NORMSINV

NORMSDST calcola il valore Z e trova il suo percentile. 

DEFINE FILE GGPRODS
-* CONVERT SIZE FIELD TO DOUBLE PRECISION
X/D12.5 = SIZE;
END
TABLE FILE GGPRODS
SUM X NOPRINT CNT.X NOPRINT
-* CALCULATE MEAN AND STANDARD DEVIATION
COMPUTE NUM/D12.5 = CNT.X; NOPRINT
COMPUTE MEAN/D12.5 = AVE.X; NOPRINT
COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT
COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT 
PRINT SIZE X NOPRINT
-* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION
COMPUTE Z/D12.5 = (X - MEAN)/STDEV;
COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8');
BY PRODUCT_ID NOPRINT
END

L'emissione è:

Size              Z         NORMSD
----              -         ------
  16        -.07298         .47091
  12        -.80273         .21106
  12        -.80273         .21106
  20         .65678         .74434
  24        1.38654         .91721
  20         .65678         .74434
  24        1.38654         .91721
  16        -.07298         .47091
  12        -.80273         .21106
   8       -1.53249         .06270
Inizio pagina
x
NORMSINV: Calcolo della distribuzione normale cumulativa inversa

Come:

La funzione NORMSINV esegue calcoli su una curva di distribuzione normale standard, trovando il valore normalizzato che forma il limite superiore di un percentile in una curva di distribuzione normale standard. Si tratta dell'inverso di NORMSDST. Per informazioni su NORMSDST, consultare NORMSDST: Calcolo della distribuzione normale cumulativa standard.

I risultati di NORMSINV sono restituiti come precisione doppia e sono 6 cifre significative.
x
Sintassi: Come calcolare la funzione di distribuzione normale standard cumulativa inversa
NORMSINV(value, 'D8');

dove:

valore

Numero compreso tra 0 e 1 (che rappresenta il percentile in una normale distribuzione standard).

D8

Formato richiesto per il risultato. Il valore restituito dalla funzione è a precisione doppia. È possibile assegnarlo a un campo con qualsiasi formato numerico valido.
Esempio: Uso della funzione NORMSINV

NORMSDST trova il percentile per il campo Z. NORMSINV quindi restituisce questo percentile ad un valore normalizzato: 

DEFINE FILE GGPRODS
-* CONVERT SIZE FIELD TO DOUBLE PRECISION
X/D12.5 = SIZE;
END 
TABLE FILE GGPRODS
SUM X NOPRINT CNT.X NOPRINT
-* CALCULATE MEAN AND STANDARD DEVIATION
COMPUTE NUM/D12.5 = CNT.X; NOPRINT
COMPUTE MEAN/D12.5 = AVE.X; NOPRINT
COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT
COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT 
PRINT SIZE X NOPRINT
-* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION
-* THEN USE RETURNED VALUES AS INPUT TO NORMSINV FUNCTION
-* AND CONVERT BACK TO DATA VALUES
COMPUTE Z/D12.5 = (X - MEAN)/STDEV;
COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8');
COMPUTE NORMSI/D12.5 = NORMSINV(NORMSD, 'D8');
COMPUTE DSIZE/D12 = NORMSI * STDEV + MEAN;
BY PRODUCT_ID NOPRINT
END

L'emissione mostra che NORMSINV è l'inverso di NORMSDST e restituisce i valori originali:

Size              Z         NORMSD         NORMSI            DSIZE
----              -         ------         ------            -----
  16        -.07298         .47091        -.07298               16
  12        -.80273         .21106        -.80273               12
  12        -.80273         .21106        -.80273               12
  20         .65678         .74434         .65678               20
  24        1.38654         .91721        1.38654               24
  20         .65678         .74434         .65678               20
  24        1.38654         .91721        1.38654               24
  16        -.07298         .47091        -.07298               16
  12        -.80273         .21106        -.80273               12
   8       -1.53249         .06270       -1.53249                8
WebFOCUS