NORMSDST y NORMSINV: Cómo calcular distribuciones normales

En esta sección:

Las funciones NORMSDST y NORMSINV realizan cálculos sobre una curva de distribución normal estándar. NORMSDST calcula el porcentaje de los valores de datos que son inferiores o iguales que el valor normalizado; NORMSINV es la función inversa de NORMSDST, calcula el valor normalizado que forma el límite superior de un percentil, en una curva de distribución normal estándar.

Principio de página
x
NORMSDST: Cómo calcular la distribución normal estándar acumulativa

Cómo:

Referencia:

La función NORMSDST realiza cálculos en una curva de distribución normal estándar, estableciendo el porcentaje de los valores de datos que son inferiores o iguales que el valor normalizado. Un valor normalizado es un punto sobre el eje X de una curva de distribución normal estándar, en desviaciones estándar de la media. Esto resulta útil a la hora de determinar los percentiles en datos distribuidos normalmente.

NORMSINV es la función inversa de NORMSDST. Para más información sobre NORMSINV, consulte NORMSINV: Cómo calcular la distribución normal inversa acumulativa.

Los resultados de NORMSDST son devueltos en forma de doble precisión, con una exactitud de hasta 6 dígitos significativos.

La curva de distribución normal estándar tiene una media de 0 y una desviación estándar de 1. El área total bajo la curva es de 1. El valor normalizado es un punto en el eje X de la distribución normal estándar. Suponiendo que sus datos están distribuidos de forma normal, puede convertir un punto de datos en un valor normalizado para determinar el porcentaje de resultados que son inferiores o iguales a la puntuación directa.

Puede convertir un valor (puntuación directa) de sus datos distribuidos normalmente en el valor normalizado equivalente (puntuación z):

z = (raw_score - mean)/standard_deviation

Para convertir una puntuación z en una puntuación directa, emplee la siguiente fórmula:

raw_score = z * standard_deviation + mean

La media de los puntos de datos xi, donde i está entre 1 y n :

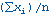
La desviación estándar de los puntos de datos xi, donde i está entre 1 y n es:

El siguiente diagrama explica los resultados de las funciones NORMSDST y NORMSINV.
x
Referencia: Características de la distribución normal

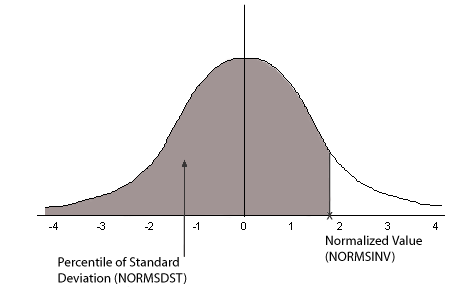
Muchas de las mediciones más frecuentes están distribuidas de forma normal. Los trazados de valores de datos distribuidos normalmente se aproximan a la curva en campana. Las dos medidas necesarias para describir cualquier distribución normal son la media y la desviación estándar:

x
Sintaxis: Cómo Calcular la función de distribución normal estándar acumulativa
NORMSDST(value, 'D8');

donde:

value

Es un valor normalizado.

D8

Es el formato obligatorio del resultado. El valor devuelto por la función es de doble precisión. Puede asignarlo a un campo con cualquier formato numérico válido.
Ejemplo: Cómo usar la función NORMSDST

NORMSDST calcula el valor Z y halla su percentil: 

DEFINE FILE GGPRODS
-* CONVERT SIZE FIELD TO DOUBLE PRECISION
X/D12.5 = SIZE;
END
TABLE FILE GGPRODS
SUM X NOPRINT CNT.X NOPRINT
-* CALCULATE MEAN AND STANDARD DEVIATION
COMPUTE NUM/D12.5 = CNT.X; NOPRINT
COMPUTE MEAN/D12.5 = AVE.X; NOPRINT
COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT
COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT 
PRINT SIZE X NOPRINT
-* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION
COMPUTE Z/D12.5 = (X - MEAN)/STDEV;
COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8');
BY PRODUCT_ID NOPRINT
END

La salida es:

Size              Z         NORMSD
----              -         ------
  16        -.07298         .47091
  12        -.80273         .21106
  12        -.80273         .21106
  20         .65678         .74434
  24        1.38654         .91721
  20         .65678         .74434
  24        1.38654         .91721
  16        -.07298         .47091
  12        -.80273         .21106
   8       -1.53249         .06270
Principio de página
x
NORMSINV: Cómo calcular la distribución normal inversa acumulativa

Cómo:

La función NORMSINV realiza cálculos en una curva de distribución normal, hallando el valor normalizado que forma el límite superior de un percentil en una curva de distribución normal estándar. Es la función inversa de NORMSDST. Para más información sobre NORMSDST, consulte NORMSDST: Cómo calcular la distribución normal estándar acumulativa.

Los resultados de NORMSINV son devueltos en forma de doble precisión, con una exactitud de hasta 6 dígitos significativos.
x
Sintaxis: Cómo Calcular la función de distribución normal estándar inversa acumulativa
NORMSINV(value, 'D8');

donde:

value

Es un número entre 0 y 1 (representa un percentil en una distribución normal estándar).

D8

Es el formato obligatorio del resultado. El valor devuelto por la función es de doble precisión. Puede asignarlo a un campo con cualquier formato numérico válido.
Ejemplo: Cómo usar la función NORMSINV

NORMSDST halla el percentil del campo Z. A continuación, NORMSINV devuelve este percentil a un valor normalizado: 

DEFINE FILE GGPRODS
-* CONVERT SIZE FIELD TO DOUBLE PRECISION
X/D12.5 = SIZE;
END 
TABLE FILE GGPRODS
SUM X NOPRINT CNT.X NOPRINT
-* CALCULATE MEAN AND STANDARD DEVIATION
COMPUTE NUM/D12.5 = CNT.X; NOPRINT
COMPUTE MEAN/D12.5 = AVE.X; NOPRINT
COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT
COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT 
PRINT SIZE X NOPRINT
-* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION
-* THEN USE RETURNED VALUES AS INPUT TO NORMSINV FUNCTION
-* AND CONVERT BACK TO DATA VALUES
COMPUTE Z/D12.5 = (X - MEAN)/STDEV;
COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8');
COMPUTE NORMSI/D12.5 = NORMSINV(NORMSD, 'D8');
COMPUTE DSIZE/D12 = NORMSI * STDEV + MEAN;
BY PRODUCT_ID NOPRINT
END

La salida muestra que NORMSINV es la función inversa de NORMSDST y que devuelve los valores originales:

Size              Z         NORMSD         NORMSI            DSIZE
----              -         ------         ------            -----
  16        -.07298         .47091        -.07298               16
  12        -.80273         .21106        -.80273               12
  12        -.80273         .21106        -.80273               12
  20         .65678         .74434         .65678               20
  24        1.38654         .91721        1.38654               24
  20         .65678         .74434         .65678               20
  24        1.38654         .91721        1.38654               24
  16        -.07298         .47091        -.07298               16
  12        -.80273         .21106        -.80273               12
   8       -1.53249         .06270       -1.53249                8
WebFOCUS