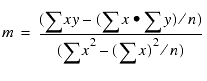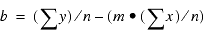Mit FORECAST
Prognose Trends berechnen und Werte vorhersagen
Sie können Trends in numerischen Daten berechnen und Werte über den Bereich der Werte hinaus, der in der Datenquelle gespeichert ist, vorhersagen, indem Sie das Feature FORECAST
Prognose verwenden. FORECAST kann in einer Report- oder Diagrammanfrage verwendet werden.
Die Berechnungen, die Sie durchführen können, um Trends und Prognosewerte zu identifizieren, lauten:
-
Einfacher gleitender Durchschnitt (MOVAVE).
Einfacher gleitender Durchschnitt. Berechnet eine Reihe arithmetischer Mittel mit einer angegebenen Werteanzahl aus einem Feld. Genaueres finden Sie unter Einen einfachen gleitenden Durchschnitt verwenden
Einen einfachen gleitenden Durchschnitt verwenden.
-
Exponentieller gleitender Durchschnitt. Berechnet einen gewichteten Durchschnitt zwischen dem zuvor berechneten Wert des Durchschnitts und dem nächsten Datenpunkt. Es gibt drei Methoden, um einen exponentiellen gleitenden Durchschnitt zu verwenden:
-
Analyse der linearen Regression (REGRESS).
Analyse der linearen Regression. Leitet die Koeffizienten einer geraden Linie ab, die für die Datenpunkte am besten passt, und verwendet diese lineare Gleichung, um Werte zu schätzen. Genaueres finden Sie unter Verwendungshinweise für die Erstellung von virtuellen Feldern.
Wenn Sie zusätzlich zum Berechnen von Trends Werte vorhersagen, fährt FORECAST
Prognose mit denselben Berechnungen über die Datenpunkte hinaus fort, indem die erzeugten Trendwerte als neue Datenpunkte verwendet werden. Für die Methode Lineare Regression wird die berechnete Regressionsgleichung verwendet, um Trendwerte und vorhergesagte Werte abzuleiten.
FORECAST
Prognose führt die Berechnungen basierend auf den bereitgestellten Daten durch, aber für Entscheidungen über ihre Verwendung und Zuverlässigkeit ist der Benutzer zuständig. Daher sind FORECAST
Prognose-Vorhersagen nicht immer zuverlässig, und viele Faktoren bestimmen, wie präzise eine Vorhersage ist.
x
FORECAST-Verarbeitung
Prognoseverarbeitung
Vorgehensweise: Referenz: |
Sie rufen FORECAST
Prognose-Verarbeitung auf, indem Sie FORECAST
Prognose in einen RECAP-Befehl
eine Recap-Formel aufnehmen. In diesem Befehl geben Sie die Parameter an, die nötig sind, um geschätzte Werte zu erzeugen, einschließlich des Feldes, das in den Berechnungen verwendet werden soll, dem Berechnungstyp, der verwendet werden soll, und der Anzahl der Vorhersagen, die erzeugt werden sollen. Das Feld RECAP
Recap, das das Ergebnis von FORECAST
Prognose enthält, kann ein neues Feld sein (nicht rekursiv) oder dasselbe Feld, das in den FORECAST
Prognose-Berechnungen verwendet wird (rekursiv):
- In einer rekursiven FORECAST
Prognose ist das Feld RECAP
Recap, das die Ergebnisse enthält, auch das Feld, das verwendet wird, um die FORECAST
Prognose-Berechnungen zu erzeugen. In diesem Fall wird das ursprüngliche Feld nicht gedruckt, selbst wenn darauf im Anzeigebefehl verwiesen wurde, und die Spalte RECAP
Recap enthält die ursprünglichen Feldwerte gefolgt von der Anzahl der vorhergesagten Werte, die in der FORECAST
Prognose-Syntax angegeben sind. Es werden im Report keine Trendwerte angezeigt. Es wird jedoch die ursprüngliche Spalte in einer Ausgabedatei gespeichert, es sei denn Sie stellen HOLDLIST auf PRINTONLY ein.
- In einer nicht rekursiven FORECAST
Prognose enthält ein neues Feld die Ergebnisse von FORECAST
Prognose-Berechnungen. Das neue Feld wird im Report zusammen mit dem ursprünglichen Feld angezeigt, wenn darauf im Anzeigebefehl verwiesen wird. Das neue Feld enthält Trendwerte und Prognosewerte wenn angegeben.
FORECAST
Prognose wird mit dem letzten ACROSS
Across-Feld in der Anfrage durchgeführt. Wenn die Anfrage kein ACROSS
Across-Feld enthält, wird das letzte BY
By-Feld verwendet. Die FORECAST
Prognose-Berechnungen fangen neu an, wenn das Sortierfeld der höchsten Ebene seinen Wert ändert. In einer Anfrage mit mehreren Anzeigebefehlen wird FORECAST
Prognose mit dem letzten ACROSS
Across-Feld durchgeführt (oder wenn keine ACROSS
Across-Felder vorhanden sind m it dem letzten BY
By-Feld) des letzten Anzeigebefehls. Wenn Sie ein ACROSS-Feld mit FORECAST verwenden, muss der Anzeigebefehl SUM oder COUNT lauten.
Wenn Sie ein Across-Feld mit Prognose verwenden, muss das Feld ein Summenfeld sein.
Hinweis: Obwohl Sie Parameter an FORECAST
Prognose mit einer Argumentliste in Klammern weiterreichen, ist FORECAST
Prognose keine Funktion. Es kann gemeinsam mit einer Funktion mit demselben Namen verwendet werden, solange die Funktion nicht in einem RECAP-Befehl
einer Recap-Formel angegeben wird.
x
Syntax: Trends berechnen und Werte vorhersagen
MOVAVE-Berechnung
ON sortfield RECAP result_field[/fmt] = FORECAST(infield, interval,
npredict, 'MOVAVE',npoint1)sendstyle
EXPAVE-Berechnung
ON sortfield RECAP result_field[/fmt] = FORECAST(infield, interval,
npredict, 'EXPAVE',npoint1);
DOUBLEXP-Berechnung
ON sortfield RECAP fld1[/fmt] = FORECAST(infield,
interval, npredict, 'DOUBLEXP',npoint1, npoint2);
SEASONAL-Berechnung
ON sortfield RECAP fld1[/fmt] = FORECAST(infield,
interval, npredict, 'SEASONAL', nperiod, npoint1, npoint2, npoint3);
REGRESS-Berechnung
ON sortfield RECAP result_field[/fmt] = FORECAST(infield, interval,
npredict, 'REGRESS');
Hierbei gilt:
- sortfield
- Ist das letzte ACROSS-Feld in der Anfrage. Dieses Feld muss sich in numerischem Format oder Datumsformat befinden. Wenn die Anfrage kein ACROSS-Feld enthält, funktioniert FORECAST mit dem letzten BY-Feld.
- result_field
- Ist das Feld, das das Ergebnis von FORECAST enthält. Es kann sich um ein neues Feld handeln oder dasselbe wie infield. Dies muss ein numerisches Feld sein; entweder ein reales Feld, ein virtuelles Feld oder ein berechnetes Feld.
Hinweis: Das Wort FORECAST und die öffnende Klammer müssen sich auf derselben Zeile wie die Syntax sortfield= befinden.
- fmt
- Ist das Anzeigeformat für result_field. Das Defaultformat lautet D12.2. Wenn result_field zuvor neu formatiert wurde mit einem DEFINE- oder COMPUTE-Befehl, wird das Format beachtet, das im RECAP-Befehl angegeben ist.
- infield
- Ist ein numerisches Feld. Es kann dasselbe Feld sein wie result_field oder ein anderes Feld. Es kann kein Datum-Zeit-Feld oder ein numerisches Feld mit Optionen für die Datumsanzeige sein.
- interval
- Ist das Inkrement, das jedem sortfield-Wert hinzugefügt werden soll (nach dem letzten Datenpunkt), um den nächsten Wert zu erstellen. Dies muss eine positive ganze Zahl sein. Um in absteigender Reihenfolge zu sortieren, verwenden Sie die Phrase BY HIGHEST. Nachdem Sie die Zahl den sortfield-Werten hinzugefügt haben wird das Ergebnis in dasselbe Format umgewandelt wie sortfield.
Bei Datumsfelder bestimmt die minimale Komponente im Format, wie die Zahl interpretiert wird. Wenn beispielsweise das Format YMD, MDY oder DMY lautet, wird ein Intervallwert von 2 als zwei Tage interpretiert. Wenn das Format YM lautet, wird 2 als zwei Monate interpretiert.
- npredict
- Ist die Anzahl der Vorhersagen, die FORECAST berechnen soll. Es muss eine ganze Zahl sein, die größer als oder gleich Null ist. Null bedeutet, dass Sie keine Vorhersagen wünschen, und wird nur für nicht rekursive FORECASTs unterstützt. Für die Methode SEASONAL ist npredict die Anzahl der Zeiträume, die berechnet werden sollen. Die Anzahl der erzeugten Punkte ist:
nperiod * npredict
- nperiod
- Für die Methode SEASONAL ist dies eine positive ganze Zahl, die die Anzahl der Datenpunkte in einem Zeitraum angibt.
- npoint1
- Ist die Anzahl der Werte, deren Durchschnitt für die Methode MOVAVE berechnet werden soll. Für EXPAVE, DOUBLEXP und SEASONAL wird diese Zahl verwendet, um die Gewichtung für jede Komponente im Durchschnitt zu berechnen. Dieser Wert muss eine positive ganze Zahl sein. Die Gewichtung k wird mit der folgenden Formel berechnet:
k=2/(1+npoint1)
- npoint2
- Für DOUBLEXP und SEASONAL wird diese positive ganze Zahl verwendet, um die Gewichtung für jeden Abschnitt im Trend zu berechnen. Die Gewichtung g wird mit der folgenden Formel berechnet:
g=2/(1+npoint2)
- npoint3
- Für DOUBLEXP und SEASONAL wird diese positive ganze Zahl verwendet, um die Gewichtung für jeden Abschnitt in der saisonalen Anpassung zu berechnen. Die Gewichtung p wird mit der folgenden Formel berechnet:
p=2/(1+npoint3)
x
Referenz: Verwendungshinweise für FORECAST
Prognose
- Das Sortierfeld, das für FORECAST
Prognose verwendet wird, muss sich in einem numerischen Format oder einem Datumsformat befinden.
- Wenn Sie Methoden für einfache bewegliche Durchschnitte und exponentielle bewegliche Durchschnitte verwenden, sollten Datenwerte gleichmäßig verteilt werden, um aussagekräftige Ergebnisse zu erhalten.
- Wenn Sie einen RECAP-Befehl
eine Recap-Formel mit FORECAST
Prognose verwenden, kann der Befehl
die Formel nur die FORECAST-Syntax
Prognoseformel enthalten. FORECAST
Prognose erkennt keine Syntax nach dem schließenden Semikolon (;). Um Optionen wie AS oder IN anzugeben:
- Verwenden Sie in einer nicht rekursiven FORECAST
Prognose-Anfrage einen leeren COMPUTE-Befehl
eine leere Compute-Formel vor RECAP
der Recap-Formel.
- Geben Sie in einer rekursiven FORECAST
Prognose-Anfrage die Optionen an, wenn auf das Feld zum ersten Mal in der Reportanfrage verwiesen wird.
- Die Verwendung der Spaltennotation wird in einer Anfrage, die FORECAST
Prognose enthält, nicht unterstützt. Wenn Sie FORECAST
Prognose-Werte erzeugen, werden zusätzliche Spalten erstellt, die in der Reportausgabe nicht gedruckt werden. Die Anzahl und Platzierung dieser zusätzlichen Spalten hängt von der spezifischen Anfrage ab.
- Eine Anfrage kann bis zu sieben nicht FORECAST
Prognose
RECAP-Befehle
Recap-Formeln enthalten und bis zu sieben zusätzliche FORECAST RECAP-Befehle
Prognose-Recap-Formeln.
- Die linke Seite eines RECAP-Befehls
einer Recap-Formel für FORECAST
Prognose unterstützt das Attribut CURR für die Erstellung eines Feldes mit benannter Währung.
- Rekursive und nicht rekursive REGRESSs werden nicht in derselben Anfrage unterstützt, wenn der Anzeigebefehl SUM, ADD oder WRITE lautet.
- Fehlende Werte werden mit REGRESS nicht unterstützt.
- Wenn Sie den Parameter ESTRECORDS verwenden, um die externe Sortierung zu aktivieren, um besser abschätzen zu können, wie viel Platz benötigt wird, müssen Sie beachten, dass FORECAST
Prognose mit Vorhersagen zusätzliche Datensätze in der Ausgabe erstellt.
- In einem Report mit Styling können Sie Werten spezifische Attribute zuweisen, die durch FORECAST
Prognose mit dem StyleSheet-Attribut WHEN=FORECAST vorhergesagt werden. Um beispielsweise die vorhergesagten Werte in rot anzuzeigen, verwenden Sie die folgende Syntax in der TABLE-Anfrage:
ON TABLE SET STYLE *TYPE=DATA,COLUMN=MYFORECASTSORTFIELD,WHEN=FORECAST,COLOR=RED,
$ENDSTYLE
x
Referenz:
FORECAST-Begrenzungen
Prognosebegrenzungen
Folgendes wird mit einem RECAP-Befehl, der FORECAST verwendet, nicht unterstützt:
Folgendes wird mit Prognose (in einer Recap-Formel) nicht unterstützt:
- Mit Daten in einem der Smart-Datumsformate sortieren (basierend auf YYMD).
- BY TOTAL-Befehl.
- MORE-, MATCH-, FOR- und OVER-Phrasen.
- SUMMARIZE und RECOMPUTE werden nicht unterstützt für dasselbe Sortierfeld, das für FORECAST verwendet wird.
- MISSING-Attribut.
xEinen einfachen gleitenden Durchschnitt verwenden
Vorgehensweise: Referenz: |
Ein einfacher gleitender Durchschnitt ist eine Reihe arithmetischer Mittel, die mit einer bestimmten Wertanzahl von einem Feld berechnet werden. Jedes neue Mittel in der Reihe wird berechnet, indem der erste Wert, der in der vorherigen Berechnung verwendet wurde, verworfen wird, und der nächste Datenwert der Berechnung hinzugefügt wird.
Einfache gleitende Durchschnitte werden manchmal verwendet, um Trends von Aktienpreisen über einen Zeitraum hinweg zu analysieren. In diesem Szenario wird der Durchschnitt mit einer angegebenen Anzahl von Zeiträumen von Aktienpreisen berechnet. Ein Nachteil dieses Indikators ist, dass er im Laufe der Zeit Daten verliert, da er immer den ältesten Wert in der Berechnung verwirft. Mittelwerte werden auch durch extreme Höchst- und Tiefstwerte verzerrt, da diese Methode allen Punkten dieselbe Gewichtung gibt.
Vorhergesagte Werte über den Bereich der Datenwerte hinaus werden berechnet mit dem gleitenden Durchschnitt, der die berechneten Trendwerte als neue Datenpunkte behandelt.
Der erste vollständige gleitende Durchschnitt tritt auf am nten Datenpunkt, da die Berechnung n Werte benötigt. Dies wird als Verzögerung bezeichnet. Die Werte für den gleitenden Durchschnitt für die Verzögerungszeilen werden wie folgt berechnet: der erste Wert in der Spalte Gleitender Durchschnitt ist identisch mit dem ersten Datenwert, der zweite Wert in der Spalte Gleitender Durchschnitt ist der Durchsschnitt der ersten beiden Datenwerte, usw., bis zur nten Zeile. Zu diesem Zeitpunkt stehen genug Werte bereit, um den gleitenden Durchschnitt mit der angegebenen Wertanzahl zu berechnen.
Beispiel: Eine neue Einfacher gleitender Durchschnitt-Spalte berechnen
Diese Anfrage definiert einen ganzzahligen Wert namens PERIOD, der als unabhängige Variable für den gleitenden Durchschnitt verwendet wird. Sie sagt drei Werteperioden über den Bereich der abgerufenen Daten hinaus voraus.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM UNITS DOLLARS
BY CATEGORY BY PERIOD
WHERE SYEAR EQ 97 AND CATEGORY NE 'Gifts'
ON PERIOD RECAP MOVAVE/D10.1= FORECAST(DOLLARS,1,3,'MOVAVE',3);
END
Die Ausgabe ist:
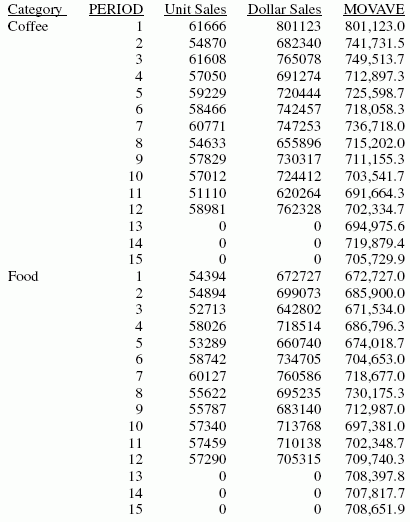
Im Report ist die Anzahl der Werte, die verwendet werden sollen, 3, und es gibt keine UNITS- oder DOLLARS-Werte für die erzeugten PERIOD-Werte.
Jeder Durchschnitt (MOVAVE-Wert) wird berechnet mit DOLLARS-Werten, wo diese vorhanden sind. Die Berechnung des gleitenden Durchschnitts beginnt folgendermaßen:
- Der erste MOVAVE-Wert (801.123,0) ist identisch mit dem ersten DOLLARS-Wert.
- Der zweite MOVAVE-Wert (741.731,5) ist das Mittel der DOLLARS-Werte eins und zwei: (801.123 + 682.340) /2.
- Der dritte MOVAVE-Wert (749.513,7) ist das Mittel der DOLLARS-Werte eins bis drei: (801.123 + 682.340 + 765.078) / 3.
- Der vierte MOVAVE-Wert (712.897,3) ist das Mittel der DOLLARS-Werte zwei bis vier: (682.340 + 765.078 + 691.274) /3.
Für vorhergesagte Werte über die angegebenen Werte hinaus werden die berechneten MOVAVE-Werte als neue Datenpunkte verwendet, um den gleitenden Durchschnitt fortzusetzen. Die vorhergesagten MOVAVE-Werte (angefangen mit 694.975,6 für PERIOD 13) werden berechnet mit den vorherigen MOVAVE-Werten als neue Datenpunkte. Beispielsweise ist der erste vorhergesagte Wert (694.975,6) der Durchschnitt der Datenpunkte der Perioden 11 und 12 (620.264 und 762.328) und der gleitende Durchschnitt für Periode 12 (702.334,7). Die Berechnung lautet: 694.975 = (620.264 + 762.328 + 702.334.7)/3.
Beispiel: Ein vorhandenes Feld als Einfacher gleitender Durchschnitt-Spalte verwenden
Diese Anfrage definiert einen ganzzahligen Wert namens PERIOD, der als unabhängige Variable für den gleitenden Durchschnitt verwendet wird. Sie sagt drei Werteperioden über den Bereich der abgerufenen Daten hinaus voraus. Sie verwendet denselben Namen für das RECAP-Feld wie das erste Argument in der FORECAST-Parameterliste. Die Trendwerte werden im Report nicht angezeigt. Auf die tatsächlichen Datenwerte für DOLLARS folgen die vorhergesagten Werte in der Reportspalte.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM UNITS DOLLARS
BY CATEGORY BY PERIOD
WHERE SYEAR EQ 97 AND CATEGORY NE 'Gifts'
ON PERIOD RECAP DOLLARS/D10.1 = FORECAST(DOLLARS,1,3,'MOVAVE',3);
END
Die Ausgabe ist:
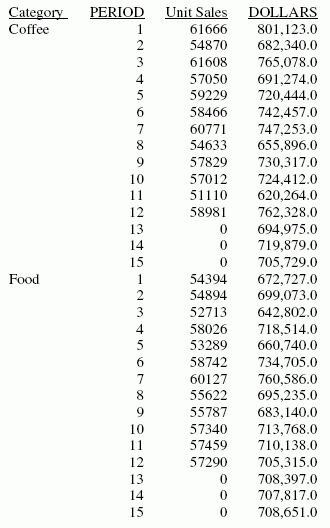
x
Vorgehensweise: Einen einfachen gleitenden Durchschnitt berechnen
-
Klicken Sie mit dem By- oder Across-Feld, das Sie für Ihre Berechnungen verwenden möchten, auf Prognose.
Die Dialogbox Prognose wird geöffnet.
-
Wenn Sie den Namen des Ausgabefeldes ändern möchten, das die prognostizierten Werte anzeigt, bearbeiten Sie den Defaultnamen, der im Feld Feldname vorhanden ist.
-
Klicken Sie auf Gleitender Durchschnitt in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
-
Wählen Sie eine Eingabemessgröße in der Dropdown-Liste Schritt 2: Eine Messgröße wählen.
Wenn Sie dasselbe Feld auswählen wie das By- oder Across-Feld, wird dieses Feld in der Ausgabe nicht angezeigt, selbst wenn es in einen Anzeigebefehl aufgenommen wird.
-
Wählen Sie die laufende Nummer im Menü Schritt 3: Das Intervall auswählen aus, um jede Instanz des By- oder Across-Feldes zu zählen.
-
Wählen Sie im Menü Schritt 4: Anzahl der Prognosen auswählen aus, wie viele Vorhersagen für das Feld Prognose berechnet werden sollen.
-
Wählen Sie im Menü Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll aus, für wie viele Werte der Durchschnitt berechnet werden soll.
-
Ändern Sie optional das Default-Feldformat, indem Sie auf den Button Format ändern klicken und ein anderes Format in der Dialogbox Format auswählen.
-
Klicken Sie auf OK.
x
Referenz: Dialogbox Prognose - Gleitender Durchschnitt
Die Dialogbox Prognose ist in der folgenden Abbildung zu sehen.
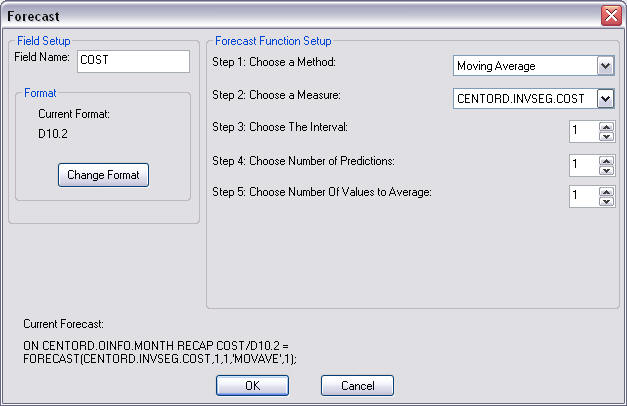
Die Dialogbox Prognose enthält die folgenden Felder oder Optionen.
Feld-Setup
-
Feldname
- Ist der Prognose-Feldname.
-
Aktuelles Format
- Zeigt das Format der Prognose an.
-
Format ändern
- Öffnet die Dialogbox Format.
-
Setup der Prognosefunktion
-
Step 1: Eine Methode auswählen
- Ist die Prognosemethode, die verwendet werden soll, um Werte vorherzusagen. Die Optionen sind:
Doppelter exponentieller Durchschnitt. Sorgt dafür, dass die Daten mit der Zeit entweder zunehmen oder abnehmen, ohne wiederholt zu werden.
Exponentieller Durchschnitt. Berechnet einen gewichteten Durchschnitt zwischen dem zuvor berechneten Wert des Durchschnitts und dem nächsten Datenpunkt.
Lineare Regression. Leitet die Koeffizienten einer geraden Linie ab, die für die Datenpunkte am besten passt, und verwendet diese lineare Gleichung, um Werte zu schätzen.
Gleitender Durchschnitt. Berechnet eine Reihe arithmetischer Mittel mit einer angegebenen Werteanzahl aus einem Feld.
Multivariate Regression. Sagt zwei oder mehr abhängige Variable mithilfe einer unabhängigen Variable voraus.
Dreifacher exponentieller Durchschnitt. Sorgt dafür, dass die Daten sich mit der Zeit wiederholen.
-
Schritt 2: Eine Messgröße auswählen
- Ist das Feld, das verwendet werden soll, um das Feld Prognose zu berechnen.
-
Schritt 3: Das Intervall auswählen
- Ist das Intervall, in dem Instanzen des By- oder Across-Feldes gezählt werden.
-
Schritt 4: Anzahl der Prognosen auswählen
- Ist die Anzahl der Vorhersagen, die berechnet werden sollen.
-
Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll
- Ist die Anzahl der Werte, die verwendet werden, um den Durchschnitt zu berechnen, der verwendet wird, um Werte vorherzusagen.
-
Aktuelle Prognose
- Zeigt den Code an, der von der Dialogbox Prognose erstellt wird.
Beispiel: Einen einfachen gleitenden Durchschnitt berechnen
Erstellen Sie eine neue Prozedur, öffnen Sie sie mit dem Report Painter und öffnen Sie die Datei centord.mas.
- Wählen Sie Report oben im ReportPainter-Fenster aus, und wählen Sie dann Define in der Dropdown-Liste aus.
Die Dialogbox Define wird geöffnet.
- Geben Sie PERIOD in den Eingabebereich Feld ein, geben Sie I2 (Ganze Zahl-Format) in den Eingabebereich Format ein, doppelklicken Sie dann auf MONTH in der Felderliste, um dies dem Bereich unter PERIOD hinzuzufügen, und klicken Sie dann auf OK.
- Fügen Sie dem Report die Felder PERIOD, REGION, QUANTITY und LINE_COGS hinzu.
- Wählen Sie das Feld PERIOD aus und klicken Sie auf den Button By.
- Wählen Sie das Feld QUANTITY aus und klicken Sie auf den Button Sum.
- Klicken Sie auf den Button Where im Button Where/If.
Der Expression Builder wird geöffnet.
- Wählen Sie REGION im Datenabschnitt aus.
- Geben Sie REGION EQ 'WEST' in den Abschnitt Erweitert ein und klicken Sie auf OK.
- Klicken Sie auf den Button Prognose.
Die Dialogbox Prognose wird geöffnet.
- Geben Sie in das Feld Feldname MOVING_AVE ein.
- Wählen Sie Gleitender Durchschnitt in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
- Wählen Sie LINE_COGS im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
- Geben Sie 1 an im Menü Schritt 3: Das Intervall auswählen.
- Geben Sie 3 an im Schritt 4: Anzahl der Prognosen auswählen-Menü.
- Geben Sie 3 an im Menü Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll.
- Klicken Sie auf OK.
- Führen Sie den Report aus.
Die Ausgabe wird im folgenden Bild illustriert.
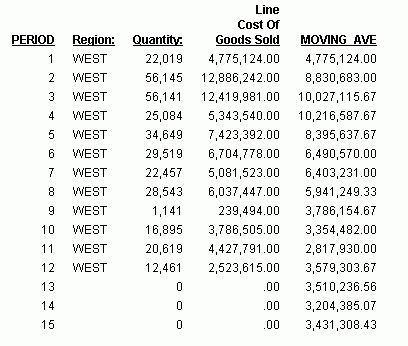
Im Report ist die Anzahl der erzeugten Werte, die für den gleitenden Durchschnitt verwendet werden sollen, 3, und es gibt keine REGION-, QUANTITY- oder LINE_COGS-Werte für die erzeugten PERIOD- und MOVING_AVE-Felder.
Jedes MOVING_AVE-Feld wird berechnet, indem die drei vorherigen LINE_COGS-Werte addiert und die Summe durch drei geteilt wird. Wenn Sie in die Zukunft gehen, in der kein LINE_COGS-Wert verfügbar ist, wird der Wert des letzten berechneten MOVING_AVE anstelle des fehlenden LINE_COGS-Werts verwendet. Die Berechnungen des erzeugten gleitenden Durchschnitts werden hier beschrieben:
- Der zwölfte MOVING_AVE-Wert (3.579.303,67) ist identisch mit dem Durchschnitt der LINE_COGS-Werte für die PERIODs 10, 11 und 12. Die Berechnung lautet (3.786.505,00 + 4.427.791,00 + 2.523.615,00)/3.
- Der dreizehnte MOVING AVE-Wert (3.510.236,56) ist identisch mit dem Durchschnitt der LINE_COGS-Werte für die PERIODs 11, 12 und 13 (wobei der zwölfte MOVING_AVE-Wert verwendet wird für den Nullwert LINE_COGS für PERIOD 13). Die Berechnung lautet (4.427.791,00 + 2.523.615,00 + 3.579.303,67)/3.
- Der vierzehnte MOVING AVE-Wert (3.204.385,07) ist identisch mit dem Durchschnitt der LINE_COGS-Werte für die PERIODs 12, 13 und 14 (wobei der zwölfte und dreizehnte MOVING_AVE-Wert verwendet werden für die Nullwerte LINE_COGS für die PERIODs 13 und 14). Die Berechnung lautet (2.523.615,00 + 3.579.303,67 + 3.510.236,56)/3.
- Der fünfzehnte MOVING AVE-Wert (3.431.308,43) ist identisch mit dem Durchschnitt der LINE_COGS-Werte für die PERIODs 13, 14 und 15 (wobei der dreizehnte und vierzehnte MOVING_AVE-Wert verwendet werden für die Nullwerte LINE_COGS für die PERIODs 14 und 15). Die Berechnung lautet (3.579.303,67 + 3.510.236,56 + 3.204.385,07)/3.
xEinfache exponentielle Glättung verwenden
Vorgehensweise: Referenz: |
Die Einfache exponentielle Glättung-Methode berechnet einen Durchschnitt, der es Ihnen ermöglicht, Gewichtungen auszuwählen, die auf neuere und ältere Werte angewendet werden sollen.
Die folgende Formel bestimmt die Gewichtung, die dem neuesten Wert gegeben wird.
k = 2/(1+n)
Hierbei gilt:
- k
- Ist der neueste Wert.
- n
- Ist eine ganze Zahl größer als eins. Wenn Sie n erhöhen, wird die Gewichtung erhöht, die den vorherigen Beobachtungen (oder Dateninstanzen) zugewiesen wurde, gegenüber den späteren.
Die nächste Berechnung des Exponentieller gleitender Durchschnitt-Werts (EMA) wird abgeleitet mit der folgenden Formel:
EMA = (EMA * (1-k)) + (datavalue * k)
Dies bedeutet, dass der neueste Wert aus der Datenquelle multipliziert wird mit dem Faktor k und der aktuelle gleitende Durchschnitt wird multimpliziert mit dem Faktor (1-k). Diese Mengen werden dann summiert, um den neuen exponentiellen gleitenden Durchschnitt (EMA) zu erzeugen.
Hinweis: Wenn es keine weiteren Datenwerte gibt, wird der letzte Datenwert in der Sortiergruppe als nächster Datenwert verwendet.
Beispiel: Eine Einfache exponentielle Glättung-Spalte berechnen
Nachfolgendes definiert einen ganzzahligen Wert namens PERIOD, der als unabhängige Variable für den gleitenden Durchschnitt verwendet wird. Sie sagt drei Werteperioden über den Bereich der abgerufenen Daten hinaus voraus.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM UNITS DOLLARS
BY CATEGORY BY PERIOD
WHERE SYEAR EQ 97 AND CATEGORY NE 'Gifts'
ON PERIOD RECAP EXPAVE/D10.1= FORECAST(DOLLARS,1,3,'EXPAVE',3);
END
Die Ausgabe ist:
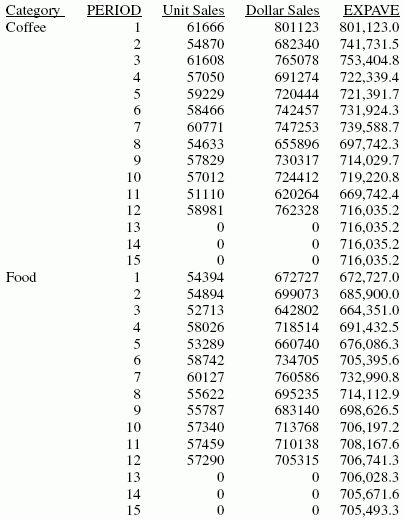
Im Report werden drei vorhergesagte Werte von EXPAVE innerhalb jedes Werts von CATEGORY berechnet. Für Werte außerhalb des Datenbereichs werden neue PERIOD-Werte erzeugt, indem der Intervallwert (1) dem vorherigen PERIOD-Wert hinzugefügt wird.
Jeder Durchschnitt (EXPAVE-Wert) wird berechnet mit DOLLARS-Werten, wo diese vorhanden sind. Die Berechnung des gleitenden Durchschnitts beginnt folgendermaßen:
- Der erste EXPAVE-Wert (801.123,0) ist identisch mit dem ersten DOLLARS-Wert.
- Der zweite EXPAVE-Wert (741.731,5) wird wie folgt berechnet. Beachten Sie, dass der Wert, der in dieser einfachen Berechnung abgeleitet wird, sich aufgrund von Rundung und der verwendeten Anzahl von Dezimalstellen leicht von dem Wert unterscheidet, der in der Reportausgabe angezeigt wird:
n=3 (number used to calculate weights)
k = 2/(1+n) = 2/4 = 0.5
EXPAVE = (EXPAVE*(1-k))+(new-DOLLARS*k) = (801123*0.5) + (682340*0.50) = 400561.5 + 341170 = 741731.5
- Der dritte EXPAVE-Wert (753.404,8) wird wie folgt berechnet:
EXPAVE = (EXPAVE*(1-k))+(new-DOLLARS*k) = (741731.5*0.5)+(765078*0.50) = 370865.75 + 382539 = 753404.75
Für vorhergesagte Werte über die Werte hinaus, die bereitstehen, wird der Wert EXPAVE als neuer Datenpunkt in der Berechnung der exponentiellen Glättung verwendet. Die vorhergesagten EXPAVE-Werte (angefangen mit 706.741,6) werden berechnet mit dem vorherigen Durchschnitt und dem neuen Datenpunkt. Da der vorherige Durchschnitt auch als neuer Datenpunkt verwendet wird, sind die vorhergesagten Werte immer identisch mit dem letzten Trendwert. Beispielsweise ist der vorherige Durchschnitt für die Periode 13 706.741,6, und dies wird auch als der nächste Datenpunkt verwendet. Es wird daher der Durchschnitt wie folgt berechnet: (706.741,6 * 0,5) + (706.741,6 * 0,5) = 706.741,6
EXPAVE = (EXPAVE * (1-k)) + (new-DOLLARS * k) = (706741.6*0.5) +
(706741.6*0.50) = 353370.8 + 353370.8 = 706741.6
x
Vorgehensweise: Einen Einfache exponentielle Glättung-Durchschnitt berechnen
-
Klicken Sie mit dem By- oder Across-Feld, das Sie für Ihre Berechnungen verwenden möchten, auf Prognose.
Die Dialogbox Prognose wird geöffnet.
-
Wenn Sie den Namen des Ausgabefeldes ändern möchten, das die prognostizierten Werte anzeigt, bearbeiten Sie den Defaultnamen, der im Feld Feldname vorhanden ist.
-
Wählen Sie Exponentieller Durchschnitt in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
-
Wählen Sie ein Eingabefeld im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
Wenn Sie dasselbe Feld auswählen wie das By- oder Across-Feld, wird dieses Feld nicht angezeigt, selbst wenn es in einen Anzeigebefehl aufgenommen wird.
-
Wählen Sie das Intervall im Menü Schritt 3: Das Intervall auswählen aus, um jede Instanz des By- oder Across-Feldes zu zählen.
-
Wählen Sie im Menü Schritt 4: Anzahl der Prognosen auswählen aus, wie viele Vorhersagen für das Feld Prognose berechnet werden sollen.
-
Wählen Sie im Menü Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll aus, für wie viele Werte der Durchschnitt berechnet werden soll.
-
Ändern Sie optional das Default-Feldformat, indem Sie auf den Button Format ändern klicken und ein anderes Format in der Dialogbox Format auswählen.
-
Klicken Sie auf OK.
x
Referenz: Dialogbox Prognose - Exponentieller Durchschnitt
Die Dialogbox Prognose ist in der folgenden Abbildung zu sehen.
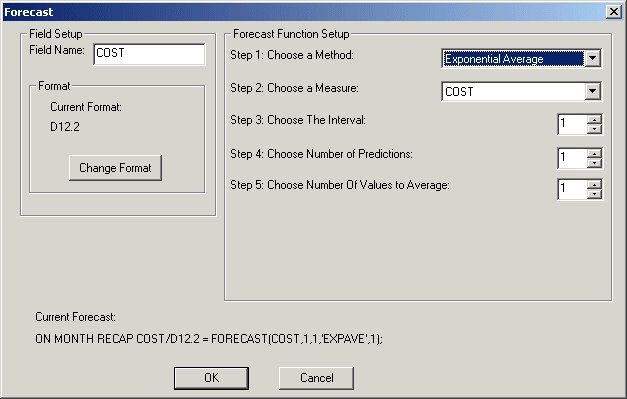
Die Dialogbox Prognose enthält die folgenden Felder oder Optionen.
-
Feld-Setup
-
Feldname
- Ist der Prognose-Feldname.
-
Aktuelles Format
- Zeigt das Prognoseformat an.
-
Format ändern
- Öffnet die Dialogbox Format.
-
Prognosefunktionen-Setup
-
Step 1: Eine Methode auswählen
- Ist die Prognosemethode, die verwendet werden soll, um Werte vorherzusagen. Die Optionen sind:
Doppelter exponentieller Durchschnitt. Sorgt dafür, dass die Daten mit der Zeit entweder zunehmen oder abnehmen, ohne wiederholt zu werden.
Exponentieller Durchschnitt. Berechnet einen gewichteten Durchschnitt zwischen dem zuvor berechneten Wert des Durchschnitts und dem nächsten Datenpunkt.
Lineare Regression. Leitet die Koeffizienten einer geraden Linie ab, die für die Datenpunkte am besten passt, und verwendet diese lineare Gleichung, um Werte zu schätzen.
Gleitender Durchschnitt. Berechnet eine Reihe arithmetischer Mittel mit einer angegebenen Werteanzahl aus einem Feld.
Multivariate Regression. Sagt zwei oder mehr abhängige Variable mithilfe einer unabhängigen Variable voraus.
Dreifacher exponentieller Durchschnitt. Sorgt dafür, dass die Daten sich mit der Zeit wiederholen.
-
Schritt 2: Eine Messgröße auswählen
- Ist das Feld, das verwendet werden soll, um das Feld Prognose zu berechnen.
-
Schritt 3: Das Intervall auswählen
- Ist das Intervall, in dem Instanzen des By- oder Across-Feldes gezählt werden.
-
Schritt 4: Anzahl der Prognosen auswählen
- Ist die Anzahl der Vorhersagen, die berechnet werden sollen.
-
Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll
- Ist die Anzahl der Werte, die verwendet werden, um den Durchschnitt zu berechnen, der verwendet wird, um Werte vorherzusagen.
-
Aktuelle Prognose
- Zeigt den Code an, der von der Dialogbox Prognose erstellt wird.
Beispiel: Einen Einfache exponentielle Glättung-Durchschnitt berechnen
Erstellen Sie eine neue Prozedur, öffnen Sie sie mit dem Report Painter und öffnen Sie die Datei centord.mas.
- Kicken Sie auf Report oben im ReportPainter-Fenster, und klicken Sie dann auf Define in der Dropdown-Liste.
Die Dialogbox Define wird geöffnet.
- Geben Sie PERIOD in den Eingabebereich Feld ein, geben Sie I2 (Ganze Zahl-Format) in den Eingabebereich Format ein, doppelklicken Sie dann auf MONTH in der Felderliste, um dies dem Bereich unter PERIOD hinzuzufügen, und klicken Sie dann auf OK.
- Fügen Sie dem Report die Felder PERIOD, REGION, QUANTITY und LINE_COGS hinzu.
- Wählen Sie das Feld PERIOD aus und klicken Sie auf den Button By.
- Wählen Sie das Feld QUANTITY aus und klicken Sie auf den Button Sum.
- Klicken Sie auf den Button Where im Dropdown-Menü Where/If.
Der Expression Builder wird geöffnet.
- Wählen Sie REGION im Datenabschnitt aus.
- Geben Sie REGION EQ 'WEST' in den Abschnitt Erweitert ein und klicken Sie auf OK.
- Klicken Sie auf den Button Prognose.
Die Dialogbox Prognose wird geöffnet.
- Geben Sie in das Feld Feldname EXP_AVE ein.
- Klicken Sie auf Exponentieller Durchschnitt in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
- Wählen Sie LINE_COGS im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
- Geben Sie 1 an im Menü Schritt 3: Das Intervall auswählen.
- Geben Sie 3 an im Schritt 4: Anzahl der Prognosen auswählen-Menü.
- Geben Sie 3 an im Menü Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll.
- Klicken Sie auf OK.
- Führen Sie den Report aus.
Wenn der Report ausgeführt wird, werden die vorhergesagten einfachen exponentiellen Werte in der EXP_AVE-Spalte angezeigt.
Die Ausgabe wird im folgenden Bild illustriert.
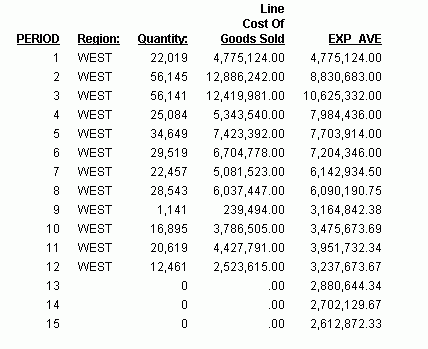
Im Report ist die Anzahl der Werte, die für jeden einfachen exponentiellen Durchschnitt verwendet werden, 3, und es gibt keine REGION-, QUANTITY- oder LINE_COGS-Werte für die erzeugten PERIOD- und EXP_AVE-Felder.
xDoppelte exponentielle Glättung verwenden
Vorgehensweise: Referenz: |
Doppelte exponentielle Glättung erzeugt einen exponentiellen gleitenden Durchschnitt, der berücksichtigt, ob die Daten im Laufe der Zeit tendenziell zunehmen oder abnehmen, ohne dass wiederholt wird. Dies wird erzielt, indem zwei Gleichungen mit zwei Konstanten verwendet werden.
Diese zwei Gleichungen werden gelöst, um den geglätteten Durchschnitt abzuleiten. Der erste geglättete Durchschnitt ist auf den ersten Datenwert eingestellt. Die erste Trendkomponente wird auf Null eingestellt. Wenn Sie die zwei Konstanten auswählen, werden die besten Ergebnisse normalerweise erzielt, indem der mittlerer quadratischer Fehler (MSE) zwischen den Datenwerten und den berechneten Durchschnitten minimiert wird. Es kann sein, dass Sie nichtlineare Optimierungsmethoden verwenden müssen, um die optimalen Konstanten zu bestimmen.
Die Gleichung, die verwendet wird, um über die Datenpunkte hinaus mit doppelter exponentieller Glättung vorherzusehen, lautet
forecast(t+m) = DOUBLEXP(t) + m * b(t)
Hierbei gilt:
- m
- Ist die Anzahl der vorhergesehenen Zeiträume für die Vorhersage.
Beispiel: Eine Doppelte exponentielle Glättung-Spalte berechnen
Nachfolgendes definiert einen ganzzahligen Wert namens PERIOD, der als unabhängige Variable für den gleitenden Durchschnitt verwendet wird. Die Methode Doppelte exponentielle Glättung schätzt den Trend der Datenpunkte besser als die Methode Einfache Glättung:
SET HISTOGRAM = OFF
TABLE FILE CENTSTMT
SUM ACTUAL_YTD
BY PERIOD
ON PERIOD RECAP EXP/D15.1 = FORECAST(ACTUAL_YTD,1,0,'EXPAVE',3);
ON PERIOD RECAP DOUBLEXP/D15.1 = FORECAST(ACTUAL_YTD,1,0,
'DOUBLEXP',3,3);
WHERE GL_ACCOUNT LIKE '3%%%'
ENDDie Ausgabe ist:
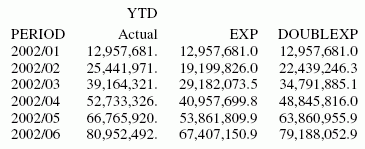
x
Vorgehensweise: Einen Doppelte exponentielle Glättung-Durchschnitt berechnen
-
Klicken Sie mit dem By- oder Across-Feld, das Sie für Ihre Berechnungen verwenden möchten, auf Prognose.
Die Dialogbox Prognose wird geöffnet.
-
Wenn Sie den Namen des Ausgabefeldes ändern möchten, das die prognostizierten Werte anzeigt, bearbeiten Sie den Defaultnamen, der im Feld Feldname vorhanden ist.
-
Wählen Sie Doppelter exponentieller Durchschnitt in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
-
Wählen Sie ein Eingabefeld im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
Wenn Sie dasselbe Feld auswählen wie das By- oder Across-Feld, wird dieses Feld nicht angezeigt, selbst wenn es in einen Anzeigebefehl aufgenommen wird.
-
Wählen Sie das Intervall im Menü Schritt 3: Das Intervall auswählen aus, um jede Instanz des By- oder Across-Feldes zu zählen.
-
Wählen Sie im Menü Schritt 4: Anzahl der Prognosen auswählen aus, wie viele Vorhersagen für das Feld Prognose berechnet werden sollen.
-
Wählen Sie im Menü Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll aus, für wie viele Werte der Durchschnitt berechnet werden soll.
-
Wählen Sie im Menü Schritt 6: Die Anzahl der Werte für jeden Trend auswählen die Zahl aus, die verwendet werden soll, um die Gewichtungen für jeden Abschnitt im Trend zu berechnen.
-
Ändern Sie optional das Default-Feldformat, indem Sie auf den Button Format ändern klicken und ein anderes Format in der Dialogbox Format auswählen.
-
Klicken Sie auf OK.
x
Referenz: Dialogbox Prognose - Doppelter exponentieller Durchschnitt
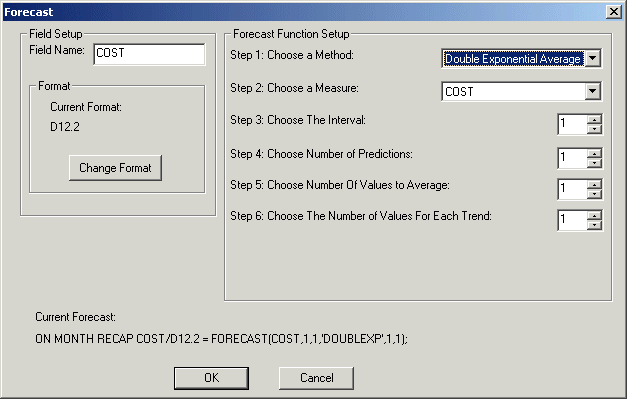
Die Dialogbox Prognose enthält die folgenden Felder oder Optionen:
Feld-Setup
-
Feldname
- Ist der Prognose-Feldname.
-
Aktuelles Format
- Zeigt das Prognoseformat an.
-
Format ändern
- Öffnet die Dialogbox Format.
Prognosefunktionen-Setup
-
Step 1: Eine Methode auswählen
- Ist die Prognosemethode, die verwendet werden soll, um Werte vorherzusagen. Die Optionen sind:
Doppelter exponentieller Durchschnitt. Sorgt dafür, dass die Daten mit der Zeit entweder zunehmen oder abnehmen, ohne wiederholt zu werden.
Exponentieller Durchschnitt. Berechnet einen gewichteten Durchschnitt zwischen dem zuvor berechneten Wert des Durchschnitts und dem nächsten Datenpunkt.
Lineare Regression. Leitet die Koeffizienten einer geraden Linie ab, die für die Datenpunkte am besten passt, und verwendet diese lineare Gleichung, um Werte zu schätzen.
Gleitender Durchschnitt. Berechnet eine Reihe arithmetischer Mittel mit einer angegebenen Werteanzahl aus einem Feld.
Multivariate Regression. Sagt zwei oder mehr abhängige Variable mithilfe einer unabhängigen Variable voraus.
Dreifacher exponentieller Durchschnitt. Sorgt dafür, dass die Daten sich mit der Zeit wiederholen.
-
Schritt 2: Eine Messgröße auswählen
- Ist das Feld, das verwendet werden soll, um das Feld Prognose zu berechnen.
-
Schritt 3: Das Intervall auswählen
- Ist das Intervall, in dem Instanzen des By- oder Across-Feldes gezählt werden.
-
Schritt 4: Anzahl der Prognosen auswählen
- Ist die Anzahl der Vorhersagen, die berechnet werden sollen.
-
Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll
- Ist die Anzahl der Werte, die verwendet werden, um den Durchschnitt zu berechnen, der verwendet wird, um Werte vorherzusagen.
-
Schritt 6: Die Anzahl der Werte für jeden Trend auswählen
- Ist die Zahl, die verwendet wird, um die Gewichtung für jeden Abschnitt im Trend zu berechnen.
Beispiel: Einen Doppelte exponentielle Glättung-Durchschnitt berechnen
Erstellen Sie eine neue Prozedur, öffnen Sie sie mit dem Report Painter und öffnen Sie die Datei centord.mas.
- Kicken Sie auf Report oben im ReportPainter-Fenster, und klicken Sie dann auf Define in der Dropdown-Liste.
Die Dialogbox Define wird geöffnet.
- Geben Sie PERIOD in den Eingabebereich Feld ein, geben Sie I2 (Ganze Zahl-Format) in den Eingabebereich Format ein, doppelklicken Sie dann auf MONTH in der Felderliste, um dies dem Bereich unter PERIOD hinzuzufügen, und klicken Sie dann auf OK.
- Fügen Sie dem Report die Felder PERIOD, REGION, QUANTITY und LINE_COGS hinzu.
- Wählen Sie das Feld PERIOD aus und klicken Sie auf den Button By.
- Wählen Sie das Feld QUANTITY aus und klicken Sie auf den Button Sum.
- Klicken Sie auf den Button Where im Dropdown-Menü Where/If.
Der Expression Builder wird geöffnet.
- Wählen Sie REGION im Datenabschnitt aus.
- Geben Sie REGION EQ 'WEST' in den Abschnitt Erweitert ein und klicken Sie auf OK.
- Klicken Sie auf den Button Prognose.
Die Dialogbox Prognose wird geöffnet.
- Geben Sie in das Feld Feldname DBL_EXP_AVE ein.
- Klicken Sie auf Doppelter exponentieller Durchschnitt in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
- Wählen Sie LINE_COGS im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
- Geben Sie 1 an im Menü Schritt 3: Das Intervall auswählen.
- Geben Sie 3 an im Schritt 4: Anzahl der Prognosen auswählen-Menü.
- Geben Sie 3 an im Menü Schritt 5: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll.
- Geben Sie 2 an im Menü Schritt 6: Die Anzahl der Werte für jeden Trend auswählen.
- Klicken Sie auf OK.
- Führen Sie den Report aus.
Wenn der Report ausgeführt wird, werden die vorhergesagten doppelten exponentiellen Werte in der DBL_EXP_AVE-Spalte angezeigt.
Die Ausgabe wird im folgenden Bild illustriert.
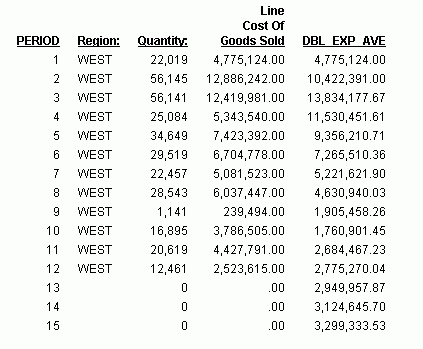
Im Report ist die Anzahl der Werte, die für jeden doppelten exponentiellen Durchschnitt verwendet werden, 3, und es gibt keine REGION-, QUANTITY- oder LINE_COGS-Werte für die erzeugten PERIOD- und DBL_EXP_AVE-Felder.
xDreifache exponentielle Glättung verwenden
Vorgehensweise: Referenz: |
Dreifache exponentielle Glättung erzeugt einen exponentiellen gleitenden Durchschnitt, der berücksichtigt, dass die Daten sich im Laufe der Zeit tendenziell wiederholen. Beispielsweise enthalten Umsatzdaten, die zunehmen, und für die 25% des Absatzes immer im Dezember zu verzeichnen sind, sowohl Trend als auch Saisonabhängigkeit. Dreifache exponentielle Glättung berücksichtigt sowohl den Trend als auch die Saisonabhängigkeit, indem drei Gleichungen mit drei Konstanten verwendet werden.
Für dreifache exponentielle Glättung müssen Sie die Anzahl der Datenpunkte in jedem Zeitraum kennen (in der folgenden Gleichung als L designiert). Um die Saisonabhängigkeit zu berücksichtigen, wird ein saisonaler Index berechnet. Die Daten werden geteilt durch den Index der vorherigen Saison und dann bei der Berechnung des geglätteten Durchschnitts verwendet.
- Die erste Gleichung berücksichtigt den aktuellen Zeitraum und ist ein gewichteter Durchschnitt des aktuellen Datenwerts, geteilt durch den saisonalen Faktor und den vorherigen Durchschnitt, angepasst für den Trend für den vorherigen Zeitraum. Die Gewichtungskonstante lautet k:
SEASONAL(t) = k * (datavalue(t)/I(t-L)) + (1-k) * (SEASONAL(t-1) + b(t-1))
- Die zweite Gleichung ist der berechnete Trendwert, und ist ein gewichteter Durchschnitt des Unterschieds zwischen dem aktuellen und dem vorherigen Durchschnitt und dem Trend für den vorherigen Zeitraum. b(t) entspricht dem durchschnittlichen Trend. Die Gewichtungskonstante lautet g:
b(t) = g * (SEASONAL(t)-SEASONAL(t-1)) + (1-g) * (b(t-1))
- Die dritte Gleichung ist der berechnete saisonale Index, und ist ein gewichteter Durchschnitt des aktuellen Datenwerts, geteilt durch den aktuellen Durchschnitt und den saisonalen Index für die vorherige Saison. I(t) steht für den durchschnittlichen saisonalen Koeffizienten. Die Gewichtungskonstante lautet p:
I(t) = p * (datavalue(t)/SEASONAL(t)) + (1 - p) * I(t-L)
Diese Gleichungen werden gelöst, um den dreifachen geglätteten Durchschnitt abzuleiten. Der erste geglättete Durchschnitt ist auf den ersten Datenwert eingestellt. Ursprüngliche Werte für die saisonalen Faktoren werden berechnet basierend auf der maximalen Anzahl vollständiger Datenperioden in der Datenquelle, wohingegen der ursprüngliche Trend basierend auf zwei Datenperioden berechnet wird. Diese Werte werden mit den folgenden Schritten berechnet:
- Der ursprüngliche Trendfaktor wird mit der folgenden Formel berechnet:
b(0) = (1/L) ((y(L+1)-y(1))/L + (y(L+2)-y(2))/L + ... + (y(2L) -
y(L))/L )
- Die Berechnung des ursprünglichen Saisonabhängigkeitsfaktors basiert auf dem Durchschnitt der Datenwerte innerhalb jeder Periode, A(j) (1<=j<=N):
A(j) = ( y((j-1)L+1) + y((j-1)L+2) + ... + y(jL) ) / L
- Dann wird der Periodizitätsfaktor mit der folgenden Formel errechnet, wobei N die Anzahl der vollständigen Perioden ist, die in den Daten verfügbar sind, L ist die Anzahl der Punkte pro Periode und n ist ein Punkt innerhalb der Periode (1<= n <= L):
I(n) = ( y(n)/A(1) + y(L+n)/A(2) + ... + y((N-1)L+n)/A(N) ) / N
Die drei Konstanten müssen vorsichtig ausgewählt werden. Die besten Ergebnisse erhält man normalerweise, indem man die Konstanten auswählt, um den mittleren quadratischen Fehler (MSE) zwischen den Datenwerten und den berechneten Durchschnitten zu minimieren. Wenn Sie die Werte für npoint1 und npoint2 variieren, wirkt sich das auf die Ergebnisse aus, und manche Werte erzeugen eine bessere Annäherung. Für eine bessere Annäherung sollten Sie Werte finden, die den mittleren quadratischen Fehler minimieren.
Die Gleichung, die verwendet wird, um über den letzten Datenpunkt hinaus mit dreifacher exponentieller Glättung vorherzusehen, lautet:
forecast(t+m) = (SEASONAL(t) + m * b(t)) / I(t-L+MOD(m/L))
Hierbei gilt:
- m
- Ist die Anzahl der vorhergesehenen Zeiträume für die Vorhersage.
Beispiel: Eine Doppelte exponentielle Glättung-Spalte berechnen
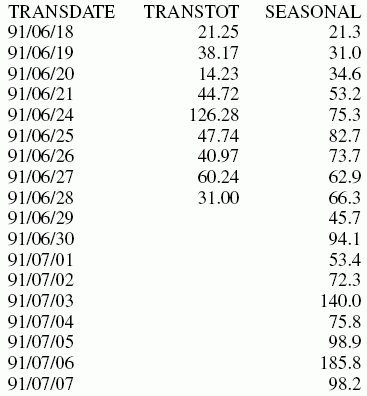
Im nachfolgenden Beispiel haben die Daten Saisonabhängigkeit, aber keinen Trend. Daher ist npoint2 hoch (1000) eingestellt, um den Trendfaktor in der Berechnung vernachlässigbar zu machen:
SET HISTOGRAM = OFF
TABLE FILE VIDEOTRK
SUM TRANSTOT
BY TRANSDATE
ON TRANSDATE RECAP SEASONAL/D10.1 = FORECAST(TRANSTOT,1,3,'SEASONAL',
3,3,1000,1);
WHERE TRANSDATE NE '19910617'
END
In der Ausgabe ist npredict 3. Es werden daher drei Zeiträume (neun Punkte, nperiod * npredict) erzeugt.
x
Vorgehensweise: Einen Dreifache exponentielle Glättung-Durchschnitt berechnen
-
Klicken Sie mit dem By- oder Across-Feld, das Sie für Ihre Berechnungen verwenden möchten, auf Prognose.
Die Dialogbox Prognose wird geöffnet.
-
Wenn Sie den Namen des Ausgabefeldes ändern möchten, das die prognostizierten Werte anzeigt, bearbeiten Sie den Defaultnamen, der im Feld Feldname vorhanden ist.
-
Klicken Sie auf Dreifacher exponentieller Durchschnitt in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
-
Wählen Sie ein Eingabefeld im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
Wenn Sie dasselbe Feld auswählen wie das By- oder Across-Feld, wird dieses Feld nicht angezeigt, selbst wenn es in einen Anzeigebefehl aufgenommen wird.
-
Wählen Sie das Intervall im Menü Schritt 3: Das Intervall auswählen aus, um jede Instanz des By- oder Across-Feldes zu zählen.
-
Wählen Sie im Menü Schritt 4: Anzahl der Prognosen auswählen aus, wie viele Vorhersagen für das Feld Prognose berechnet werden sollen.
-
Wählen Sie im Menü Schritt 5: Die Anzahl der Punkte pro Periode auswählen die Anzahl der Datenpunkte für einen Zeitraum aus.
-
Wählen Sie im Menü Schritt 6: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll aus, für wie viele Werte der Durchschnitt berechnet werden soll.
-
Wählen Sie im Menü Schritt 7: Die Anzahl der Werte für jeden Trend auswählen die Zahl aus, die verwendet werden soll, um die Gewichtungen für jeden Abschnitt im Trend zu berechnen.
-
Wählen Sie im Menü Schritt 8: Die Anzahl der Werte für saisonale Anpassung auswählen die Zahl aus, die verwendet werden soll, um die Gewichtungen für jeden Abschnitt im Trend zu berechnen.
-
Ändern Sie optional das Default-Feldformat, indem Sie auf den Button Format ändern klicken und ein anderes Format in der Dialogbox Format auswählen.
-
Klicken Sie auf OK.
x
Referenz: Dialogbox Prognose - Dreifacher exponentieller Durchschnitt
Die Dialogbox Prognose ist in der folgenden Abbildung zu sehen.
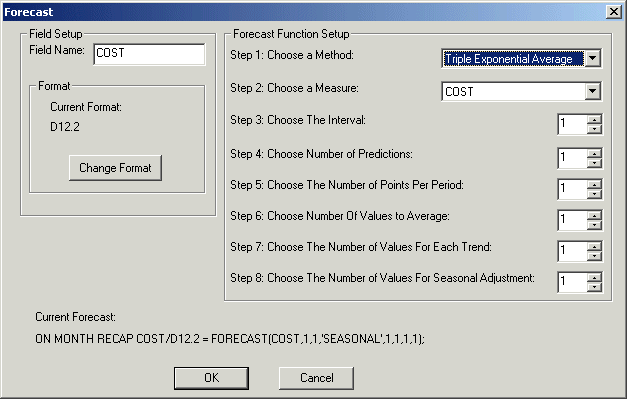
Die Dialogbox Prognose enthält die folgenden Felder oder Optionen:
Feld-Setup
-
Feldname
- Ist der Prognose-Feldname.
-
Aktuelles Format
- Zeigt das Prognoseformat an.
-
Format ändern
- Öffnet die Dialogbox Format.
Prognosefunktionen-Setup
-
Step 1: Eine Methode auswählen
- Ist die Prognosemethode, die verwendet werden soll, um Werte vorherzusagen. Die Optionen sind:
Doppelter exponentieller Durchschnitt. Sorgt dafür, dass die Daten mit der Zeit entweder zunehmen oder abnehmen, ohne wiederholt zu werden.
Exponentieller Durchschnitt. Berechnet einen gewichteten Durchschnitt zwischen dem zuvor berechneten Wert des Durchschnitts und dem nächsten Datenpunkt.
Lineare Regression. Leitet die Koeffizienten einer geraden Linie ab, die für die Datenpunkte am besten passt, und verwendet diese lineare Gleichung, um Werte zu schätzen.
Gleitender Durchschnitt. Berechnet eine Reihe arithmetischer Mittel mit einer angegebenen Werteanzahl aus einem Feld.
Multivariate Regression. Sagt zwei oder mehr abhängige Variable mithilfe einer unabhängigen Variable voraus.
Dreifacher exponentieller Durchschnitt. Sorgt dafür, dass die Daten sich mit der Zeit wiederholen.
-
Schritt 2: Eine Messgröße auswählen
- Ist das Feld, das verwendet werden soll, um das Feld Prognose zu berechnen.
-
Schritt 3: Das Intervall auswählen
- Ist das Intervall, in dem Instanzen des By- oder Across-Feldes gezählt werden.
-
Schritt 4: Anzahl der Prognosen auswählen
- Ist die Anzahl der Vorhersagen, die berechnet werden sollen.
-
Schritt 5: Die Anzahl der Punkte pro Periode auswählen
- Ist die Anzahl der Datenpunkte in einer Periode.
-
Schritt 6: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll
- Ist die Anzahl der Werte, die verwendet werden, um den Durchschnitt zu berechnen, der verwendet wird, um Werte vorherzusagen.
-
Schritt 7: Die Anzahl der Werte für jeden Trend auswählen
- Ist die Zahl, die verwendet wird, um die Gewichtung für jeden Abschnitt im Trend zu berechnen. Dieser Wert ist nur verfügbar für Doppelten exponentiellen Durchschnitt und Dreifachen exponentiellen Durchschnitt.
-
Schritt 8: Die Anzahl der Werte für saisonale Anpassung auswählen
- Ist die Zahl, die verwendet wird, um die Gewichtung für jeden Abschnitt in der saisonalen Anpassung zu berechnen.
-
Aktuelle Prognose
- Zeigt den Code an, der von der Dialogbox Prognose erstellt wird.
Beispiel: Einen Dreifache exponentielle Glättung-Durchschnitt berechnen
Erstellen Sie eine neue Prozedur, öffnen Sie sie mit dem Report Painter und öffnen Sie die Datei centord.mas.
- Kicken Sie auf Report oben im ReportPainter-Fenster, und klicken Sie dann auf Define in der Dropdown-Liste.
Die Dialogbox Define wird geöffnet.
- Geben Sie PERIOD in den Eingabebereich Feld ein, geben Sie I2 (Ganze Zahl-Format) in den Eingabebereich Format ein, doppelklicken Sie dann auf MONTH in der Felderliste, um dies dem Bereich unter PERIOD hinzuzufügen, und klicken Sie dann auf OK.
- Fügen Sie dem Report die Felder PERIOD, REGION, QUANTITY und LINE_COGS hinzu.
- Wählen Sie das Feld PERIOD aus und klicken Sie auf den Button By.
- Wählen Sie das Feld QUANTITY aus und klicken Sie auf den Button Sum.
- Klicken Sie auf den Button Where im Dropdown-Menü Where/If.
Der Expression Builder wird geöffnet.
- Wählen Sie REGION im Datenabschnitt aus.
- Geben Sie REGION EQ 'WEST' in den Abschnitt Erweitert ein und klicken Sie auf OK.
- Klicken Sie auf den Button Prognose.
Die Dialogbox Prognose wird geöffnet.
- Geben Sie in das Feld Feldname TRPL_EXP_AVE ein.
- Klicken Sie auf Dreifacher exponentieller Durchschnitt in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
- Wählen Sie LINE_COGS im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
- Geben Sie 1 an im Menü Schritt 3: Das Intervall auswählen.
- Geben Sie 3 an im Schritt 4: Anzahl der Prognosen auswählen-Menü.
- Geben Sie 3 an im Menü Schritt 5: Die Anzahl der Punkte pro Periode auswählen.
- Geben Sie 3 an im Menü Schritt 6: Auswählen, für wie viele Werte der Durchschnitt berechnet werden soll.
- Geben Sie 3 an im Menü Schritt 7: Die Anzahl der Werte für jeden Trend auswählen.
- Geben Sie 3 an im Menü Schritt 8: Die Anzahl der Werte für saisonale Anpassung auswählen.
- Klicken Sie auf OK.
- Führen Sie den Report aus.
Wenn der Report ausgeführt wird, werden die vorhergesagten dreifachen exponentiellen Werte in der TRPL_EXP_AVE-Spalte angezeigt.
Die Ausgabe wird im folgenden Bild illustriert.
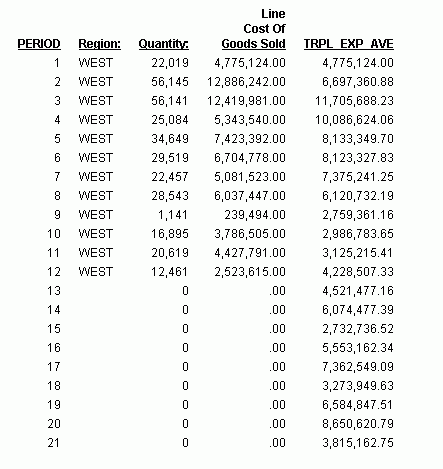
Im Report ist die Anzahl der Werte, die für jeden dreifachen exponentiellen Durchschnitt verwendet werden, 3, und es gibt keine REGION-, QUANTITY- oder LINE_COGS-Werte für die erzeugten PERIOD- und TRPL_EXP_AVE-Felder.
xEine Lineare Regressionsgleichung verwenden
Vorgehensweise: Referenz: |
Die Lineare Regressionsgleichung schätzt Werte, indem sie annimmt, dass die abhängige Variable (die neuen berechneten Werte) und die unabhängige Variable (die Sortierfeldwerte) durch eine Funktion in Beziehung stehen, die eine gerade Linie darstellt:
y = mx + b
Hierbei gilt:
- y
- Ist die abhängige Variable.
- x
- Ist die unabhängige Variable.
- m
- Ist der Anstieg der Linie.
- b
- Ist der y-Achsenabschnitt.
REGRESS verwendet eine Methode namens Gewöhnliche Kleinstquadrate, um Werte zu berechnen für m und b, die die Summe der quadrierten Differenzen zwischen den Daten und der resultierenden Linie minimieren.
In den folgenden Formeln ist zu sehen, wie m und b berechnet werden.
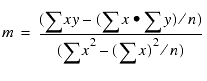
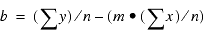
Hierbei gilt:
- n
- Ist die Anzahl der Datenpunkte.
- y
- Sind die Datenwerte (abhängige Variable).
- x
- Sind die Sortierfeldwerte (unabhängige Variable).
Sowohl Trendwerte als auch vorhergesagte Werte werden mit der Regressionsgeradengleichung berechnet.
Beispiel: Ein neues Lineare Regression-Feld berechnen
TABLE FILE CAR
PRINT MPG
BY DEALER_COST
WHERE MPG NE 0.0
ON DEALER_COST RECAP FORMPG=FORECAST(MPG,1000,3,'REGRESS');
END
Die Ausgabe ist:
DEALER_COST MPG FORMPG
2,886 27 25.51
4,292 25 23.65
4,631 21 23.20
4,915 21 22.82
5,063 23 22.63
5,660 21 21.83
21 21.83
5,800 24 21.65
6,000 24 21.38
7,427 16 19.49
8,300 18 18.33
8,400 18 18.20
10,000 18 16.08
11,000 18 14.75
11,194 9 14.50
14,940 11 9.53
15,940 0 8.21
16,940 0 6.88
17,940 0 5.55Hinweis:
- Es werden drei vorhergesagte Werte von FORMPG berechnet. Für Werte außerhalb des Datenbereichs werden neue DEALER_COST-Werte erzeugt, indem der Intervallwert (1.000) dem vorherigen DEALER_COST-Wert hinzugefügt wird.
- Es gibt keine MPG-Werte für die erzeugten DEALER_COST-Werte.
- Jeder FORMPG-Wert wird berechnet mit einer Regressionsgeraden, zu deren Berechnung alle tatsächlichen Datenwerte für MPG verwendet werden.
DEALER_COST ist die unabhängige Variable (x) und MPG ist die abhängige Variable (y). Die Gleichung wird verwendet, um den MPGFORECAST-Trend und vorhergesagte Werte zu berechnen.
In diesem Fall lautet die Gleichung etwa wie folgt:
FORMPG = (-0.001323 * DEALER_COST) + 29.32
Die vorhergesagten Werte sind (die Werte sind nicht genau so wie von FORECAST berechnet wegen Rundung, aber sie zeigen den Berechnungsvorgang).
DEALER_COST | Berechnung | FORMPG |
|---|
15,940 | (-0.001323 * 15,940) + 29.32 | 8.23 |
16,940 | (-0.001323 * 16,940) + 29.32 | 6.91 |
17,940 | (-0.001323 * 17,940) + 29.32 | 5.59 |
x
Vorgehensweise: Einen Lineare Regression-Wert berechnen
-
Klicken Sie mit dem By- oder Across-Feld, das Sie für Ihre Berechnungen verwenden möchten, auf Prognose.
Die Dialogbox Prognose wird geöffnet.
-
Wenn Sie den Namen des Ausgabefeldes ändern möchten, das die prognostizierten Werte anzeigt, bearbeiten Sie den Defaultnamen, der im Feld Feldname vorhanden ist.
-
Klicken Sie auf Lineare Regression in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
-
Wählen Sie ein Eingabefeld im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
Wenn Sie dasselbe Feld auswählen wie das By- oder Across-Feld, wird dieses Feld nicht angezeigt, selbst wenn es in einen Anzeigebefehl aufgenommen wird.
-
Wählen Sie die laufende Nummer im Menü Schritt 3: Das Intervall auswählen aus, um jede Instanz des By- oder Across-Feldes zu zählen.
-
Wählen Sie im Menü Schritt 4: Anzahl der Prognosen auswählen aus, wie viele Vorhersagen für das Feld Prognose berechnet werden sollen.
-
Ändern Sie optional das Default-Feldformat, indem Sie auf den Button Format ändern klicken und ein anderes Format in der Dialogbox Format auswählen.
-
Klicken Sie auf OK.
x
Referenz: Dialogbox Prognose - Lineare Regression
Die Dialogbox Prognose ist in der folgenden Abbildung zu sehen.
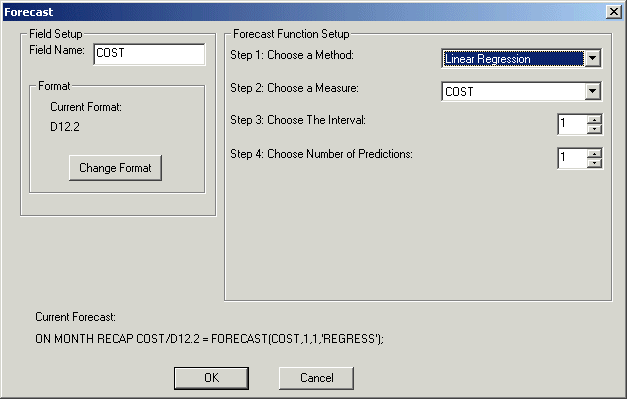
Die Dialogbox Prognose enthält die folgenden Felder oder Optionen:
Feld-Setup
-
Feldname
- Ist der Prognose-Feldname.
-
Aktuelles Format
- Zeigt das Prognoseformat an.
-
Format ändern
- Öffnet die Dialogbox Format.
Prognosefunktionen-Setup
-
Step 1: Eine Methode auswählen
- Ist die Prognosemethode, die verwendet werden soll, um Werte vorherzusagen. Die Optionen sind:
Doppelter exponentieller Durchschnitt. Sorgt dafür, dass die Daten mit der Zeit entweder zunehmen oder abnehmen, ohne wiederholt zu werden.
Exponentieller Durchschnitt. Berechnet einen gewichteten Durchschnitt zwischen dem zuvor berechneten Wert des Durchschnitts und dem nächsten Datenpunkt.
Lineare Regression. Leitet die Koeffizienten einer geraden Linie ab, die für die Datenpunkte am besten passt, und verwendet diese lineare Gleichung, um Werte zu schätzen.
Gleitender Durchschnitt. Berechnet eine Reihe arithmetischer Mittel mit einer angegebenen Werteanzahl aus einem Feld.
Multivariate Regression. Sagt zwei oder mehr abhängige Variable mithilfe einer unabhängigen Variable voraus.
Dreifacher exponentieller Durchschnitt. Sorgt dafür, dass die Daten sich mit der Zeit wiederholen.
-
Schritt 2: Eine Messgröße auswählen
- Ist das Feld, das verwendet werden soll, um das Feld Prognose zu berechnen.
-
Schritt 3: Das Intervall auswählen
- Ist das Intervall, in dem Instanzen des By- oder Across-Feldes gezählt werden.
-
Schritt 4: Anzahl der Prognosen auswählen
- Ist die Anzahl der Vorhersagen, die berechnet werden sollen.
-
Aktuelle Prognose
- Zeigt den Code an, der von der Dialogbox Prognose erstellt wird.
Beispiel: Einen linearen Regressionswert berechnen
Erstellen Sie eine neue Prozedur, öffnen Sie sie mit dem Report Painter und öffnen Sie die Datei centord.mas.
- Kicken Sie auf Report oben im ReportPainter-Fenster, und klicken Sie dann auf Define in der Dropdown-Liste.
Die Dialogbox Define wird geöffnet.
- Geben Sie PERIOD in den Eingabebereich Feld ein, geben Sie I2 (Ganze Zahl-Format) in den Eingabebereich Format ein, doppelklicken Sie dann auf MONTH in der Felderliste, um dies dem Eingabebereich unter PERIOD hinzuzufügen, und klicken Sie dann auf OK.
Die Dialogbox Define wird geschlossen und Sie kehren zum ReportPainter zurück.
- Fügen Sie dem Report die Felder PERIOD, REGION, QUANTITY und LINE_COGS hinzu.
- Wählen Sie das Feld PERIOD aus und klicken Sie auf den Button By.
- Wählen Sie das Feld QUANTITY aus und klicken Sie auf den Button Sum.
- Klicken Sie auf den Button Where im Dropdown-Menü Where/If.
Der Expression Builder wird geöffnet.
- Wählen Sie REGION im Datenabschnitt aus.
- Geben Sie REGION EQ 'WEST' in den Abschnitt Erweitert ein und klicken Sie auf OK.
- Klicken Sie auf den Button Prognose.
Die Dialogbox Prognose wird geöffnet.
- Geben Sie in das Feld Feldname LINEAR_REG ein.
- Wählen Sie Lineare Regression in der Dropdown-Liste Schritt 1: Eine Methode auswählen.
- Wählen Sie LINE_COGS im Schritt 2: Eine Messgröße-Dropdown-Liste wählen.
- Geben Sie 1 an im Menü Schritt 3: Das Intervall auswählen.
- Geben Sie 3 an im Schritt 4: Anzahl der Prognosen auswählen-Menü.
- Klicken Sie auf OK.
- Führen Sie den Report aus.
Wenn der Report ausgeführt wird, werden die vorhergesagten Lineare Regression-Werte in der Spalte LINEAR_REG angezeigt.
Die Ausgabe wird im folgenden Bild illustriert.
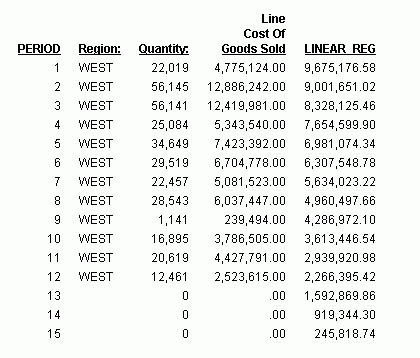
Im Report ist die Anzahl der Werte, die für jeden Lineare Regression-Wert verwendet werden, 3, und es gibt keine REGION-, QUANTITY- oder LINE_COGS-Werte für die erzeugten PERIOD- und LINEAR_REG-Felder.
x
FORECAST
Prognose-Reportmethoden
Sie können FORECAST
Prognose in einer Anfrage mehrmals verwenden. Es müssen jedoch alle FORECAST
Prognose-Anfragen dasselbe Sortierfeld, Intervall und Anzahl der Vorhersagen angeben. Es kann sich nur das RECAP
Recap-Feld ändern, die Methode, das Feld, das verwendet wird, um die FORECAST
Prognose-Werte zu berechnen, und die Anzahl der Punkte, deren Durchschnitt ermittelt werden soll. Wenn Sie einen der anderen Parameter ändern, werden die neuen Parameter ignoriert.
Wenn Sie eine FORECAST
Prognose-Spalte in der Reportausgabe verschieben möchten, verwenden Sie einen leeren COMPUTE-Befehl
eine leere Compute-Formel für das FORECAST
Prognose-Feld als Platzhalter. Der Datentyp (I, F, P, D) muss im COMPUTE-Befehl
in der Compute-Formel und dem RECAP-Befehl
der Recap-Formel identisch sein.
Um die Reportausgabe einfacher interpretieren zu können, können Sie ein Feld erstellen, das angibt, ob der FORECAST
Prognose-Wert in jeder Zeile ein vorhergesagter Wert ist. Um dies zu tun, definieren Sie ein virtuelles Feld, dessen Wert eine Konstante ist, die nicht null ist. Zeilen in der Reportausgabe, die tatsächliche Datensätze in der Datenquelle darstellen, werden mit dieser Konstanten angezeigt. Zeilen, die vorhergesagte Werte darstellen, zeigen null an. Sie können dieses Feld auch an eine HOLD-Datei weitergeben.
Beispiel: Mehrere FORECAST
Prognose-Spalten in einer Anfrage erzeugen
In diesem Beispiel werden gleitende Durchschnitte und exponentielle Durchschnitte sowohl für DOLLARS- als auch für BUDDOLLARS-Felder in der Datenquelle GGSALES berechnet. Das Sortierfeld, das Intervall und die Anzahl der Vorhersagen sind für alle Berechnungen identisch.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM DOLLARS AS 'DOLLARS' BUDDOLLARS AS 'BUDGET'
BY CATEGORY NOPRINT BY PERIOD AS 'PER'
WHERE SYEAR EQ 97 AND CATEGORY EQ 'Coffee'
ON PERIOD RECAP DOLMOVAVE/D10.1= FORECAST(DOLLARS,1,0,'MOVAVE',3);
ON PERIOD RECAP DOLEXPAVE/D10.1= FORECAST(DOLLARS,1,0,'EXPAVE',4);
ON PERIOD RECAP BUDMOVAVE/D10.1 = FORECAST(BUDDOLLARS,1,0,'MOVAVE',3);
ON PERIOD RECAP BUDEXPAVE/D10.1 = FORECAST(BUDDOLLARS,1,0,'EXPAVE',4);
END
Die Ausgabe wird im folgenden Bild illustriert.
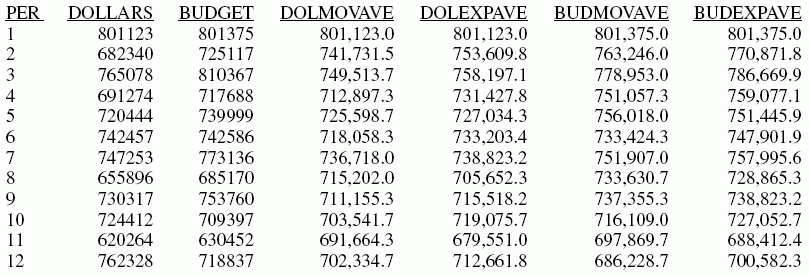
PER DOLLARS BUDGET DOLMOVAVE DOLEXPAVE BUDMOVAVE BUDEXPAVE 1 801123 801375 801,123.0 801,123.0 801,375.0 801,375.0
2 682340 725117 741,731.5 753,609.8 763,246.0 770,871.8
3 765078 810367 749,513.7 758,197.1 778,953.0 786,669.9
4 691274 717688 712,897.3 731,427.8 751,057.3 759,077.1
5 720444 739999 725,598.7 727,034.3 756,018.0 751,445.9
6 742457 742586 718,058.3 733,203.4 733,424.3 747,901.9
7 747253 773136 736,718.0 738,823.2 751,907.0 757,995.6
8 655896 685170 715,202.0 705,652.3 733,630.7 728,865.3
9 730317 753760 711,155.3 715,518.2 737,355.3 738,823.2
10 724412 709397 703,541.7 719,075.7 716,109.0 727,052.7
11 620264 630452 691,664.3 679,551.0 697,869.7 688,412.4
12 762328 718837 702,334.7 712,661.8 686,228.7 700,582.3
Beispiel: Die FORECAST-Spalte verschieben
Im folgenden Beispiel wird das Feld DOLLARS hinter das Feld MOVAVE platziert, indem ein leerer COMPUTE-Befehl als Platzhalter für das Feld MOVAVE verwendet wird. Sowohl der COMPUTE-Befehl als auch der RECAP-Befehl geben Formate für MOVAVE (desselben Datentyps) an, aber das Format das RECAP-Befehls hat Vorrang.
DEFINE FILE GGSALES
SDATE/YYM = DATE;
SYEAR/Y = SDATE;
SMONTH/M = SDATE;
PERIOD/I2 = SMONTH;
END
TABLE FILE GGSALES
SUM UNITS
COMPUTE MOVAVE/D10.2 = ;
DOLLARS
BY CATEGORY BY PERIOD
WHERE SYEAR EQ 97 AND CATEGORY EQ 'Coffee'
ON PERIOD RECAP MOVAVE/D10.1= FORECAST(DOLLARS,1,3,'MOVAVE',3);
END
Die Ausgabe wird im folgenden Bild illustriert.
Category PERIOD Unit
Sales MOVAVE Dollar
SalesCoffee 1 61666 801,123.0 801123
2 54870 741,731.5 682340
3 61608 749,513.7 765078
4 57050 712,897.3 691274
5 59229 725,598.7 720444
6 58466 718,058.3 742457
7 60771 736,718.0 747253
8 54633 715,202.0 655896
9 57829 711,155.3 730317
10 57012 703,541.7 724412
11 51110 691,664.3 620264
12 58981 702,334.7 762328
13 0 694,975.6 0
14 0 719,879.4 0
15 0 705,729.9 0
Beispiel: Datenzeilen von vorhergesagten Zeilen unterscheiden
Im folgenden Beispiel hat das virtuelle Feld DATA_ROW den Wert 1 für jede Zeile in der Datenquelle. Es hat den Wert null für die vorhergesagten Zeilen. Das PREDICT-Feld wird berechnet als YES für vorhergesagte Zeilen und NO für Zeilen, die Daten enthalten.
DEFINE FILE CAR
DATA_ROW/I1 = 1;
END
TABLE FILE CAR
PRINT DATA_ROW
COMPUTE PREDICT/A3 = IF DATA_ROW EQ 1 THEN 'NO' ELSE 'YES' ;
MPG
BY DEALER_COST
WHERE MPG GE 20
ON DEALER_COST RECAP FORMPG/D12.2=FORECAST(MPG,1000,3,'REGRESS');
ON DEALER_COST RECAP MPG =FORECAST(MPG,1000,3,'REGRESS');
END
Die Ausgabe ist:
DEALER_COST DATA_ROW PREDICT MPG FORMPG
2,886 1 NO 27.00 25.65
4,292 1 NO 25.00 23.91
4,631 1 NO 21.00 23.49
4,915 1 NO 21.00 23.14
5,063 1 NO 23.00 22.95
5,660 1 NO 21.00 22.21
1 NO 21.00 22.21
5,800 1 NO 24.20 22.04
6,000 1 NO 24.20 21.79
7,000 0 YES 20.56 20.56
8,000 0 YES 19.32 19.32
9,000 0 YES 18.08 18.08