NORMSDST e NORMSINV: Como Calcular Distribuições Normais

Nesta seção:

As funções NORMSDST e NORMSINV desempenha cálculos em uma curva de distribuição normal padrão. NORMSDST calcula a porcentagem de valores de dados que são menores ou iguais a um valor normalizado. NORMSINV é o inverso de NORMSDST e calcula o valor normalizado que forma o limite superior de um percentil em uma curva padrão de distribuição normal.

Topo da página
x
NORMSDST: Como Calcular a Distribuição Normal Acumulativa Padrão

Como:

Referência:

A função NORMSDST desempenha cálculos em uma curva de distribuição normal padrão, calculando a porcentagem de valores de dados que são menores ou iguais a um valor normalizado. Um valor normalizado é um ponto no eixo X de umacurva de distribuição normal padrão em desvios padrão a partir do meio. Isto é útil para a determinação de percentis em dados distribuídos normalmente.

A função NORMSINV é o inverso de NORMSDST. Para obter informações sobre o NORMSINV, consulte NORMSINV: Como Calculara Distribuição Normal Acumulativa Inversa.

Os resultados de NORMSDST são exibidos comosendo de precisão dupla, com precisão de seis dígitos significativos.

Uma curva de distribuição normal é uma distribuição normal que possui um meio de 0 e um desvio padrão de 1. A área total abaixo desta curva é 1. Um ponto no eixo X da distribuição normal padrão é chamado de valor normalizado. Supondo que seus dados se encontram normalmente distribuídos, você pode converter um datapoint em um valor normalizado para encontrar a porcentagem de pontos que são menores ou iguais ao ponto bruto.

Você pode converter um valor (score bruto) a partir dos seus dados distribuídos normalmente em um valor normalizado equivalente (z-score) da seguinte forma:

z = (raw_score - mean)/standard_deviation

Para converter de um score z para um score bruto, utilize a fórmula a seguir:

raw_score = z * standard_deviation + mean

O meio dos pontos de dados xi, onde i vai de 1 a n, é:

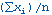
O desvio padrão dos pontos de dados xi, onde i vai de 1 a n, é:

O diagrama a seguir ilustra os resultados das funções NORMSDST e NORMSINV.
x
Referência: Características da Distribuição Normal

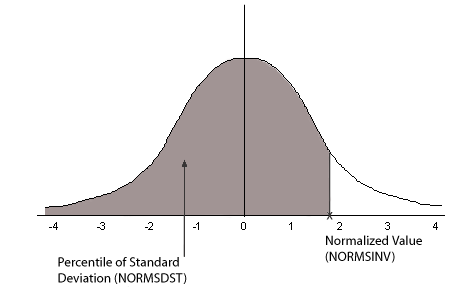
Muitas medidas comuns são distribuídas normalmente. Um diagrama de valores de dados distribuídos normalmente se assemelha a uma curva Bell. As duas medidas obrigatórias para a descrição de qualquer distribuição normal são o meio e o desvio padrão:

x
Sintaxe: Como Calcular a função de distribuição normal cumulativa padrão
NORMSDST(value, 'D8');

onde:

valor

É um valor normalizado.

D8

É o formato necessário para o resultado. O valor retornado pela função é de dupla precisão. Você pode atribuir esse valor a um campo com qualquer formato numérico válido.

Exemplo: Como Utilizar a Função NORMSDST

NORMSDST calcula o valor de Z e encontra seu percentil: 

DEFINE FILE GGPRODS
-* CONVERT SIZE FIELD TO DOUBLE PRECISION
X/D12.5 = SIZE;
END
TABLE FILE GGPRODS
SUM X NOPRINT CNT.X NOPRINT
-* CALCULATE MEAN AND STANDARD DEVIATION
COMPUTE NUM/D12.5 = CNT.X; NOPRINT
COMPUTE MEAN/D12.5 = AVE.X; NOPRINT
COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT
COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT 
PRINT SIZE X NOPRINT
-* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION
COMPUTE Z/D12.5 = (X - MEAN)/STDEV;
COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8');
BY PRODUCT_ID NOPRINT
END

A saída é:

Size              Z         NORMSD
----              -         ------
  16        -.07298         .47091
  12        -.80273         .21106
  12        -.80273         .21106
  20         .65678         .74434
  24        1.38654         .91721
  20         .65678         .74434
  24        1.38654         .91721
  16        -.07298         .47091
  12        -.80273         .21106
   8       -1.53249         .06270
Topo da página
x
NORMSINV: Como Calculara Distribuição Normal Acumulativa Inversa

Como:

A função NORMSINV desempenha cálculos em uma curva de distribuição normal padrão, encontrando o valor normalizado que forma um limite superior de um percentil em uma curva de distribuição normal padrão. Isto é o inverso de NORMSDST. Para obter informações sobre NORMSDST, consulte NORMSDST: Como Calcular a Distribuição Normal Acumulativa Padrão.

Os resultados de NORMSINV são exibidos comosendo de precisão dupla, com precisão de seis dígitos significativos.
x
Sintaxe: Como Calcular a função de distribuição normal cumulativa padrão inversa
NORMSINV(value, 'D8');

onde:

value

É um número entre 0 e 1 (que representa o percentil em uma distribuição normal padrão).

D8

É o formato necessário para o resultado. O valor retornado pela função é de dupla precisão. Você pode atribuir esse valor a um campo com qualquer formato numérico válido.

Exemplo: Como Utilizar a Função NORMSINV

NORMSDST encontra o percentil para o campo Z. NORMSINV, então, exibe este percentil para um valor normalizado: 

DEFINE FILE GGPRODS
-* CONVERT SIZE FIELD TO DOUBLE PRECISION
X/D12.5 = SIZE;
END 
TABLE FILE GGPRODS
SUM X NOPRINT CNT.X NOPRINT
-* CALCULATE MEAN AND STANDARD DEVIATION
COMPUTE NUM/D12.5 = CNT.X; NOPRINT
COMPUTE MEAN/D12.5 = AVE.X; NOPRINT
COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT
COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT 
PRINT SIZE X NOPRINT
-* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION
-* THEN USE RETURNED VALUES AS INPUT TO NORMSINV FUNCTION
-* AND CONVERT BACK TO DATA VALUES
COMPUTE Z/D12.5 = (X - MEAN)/STDEV;
COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8');
COMPUTE NORMSI/D12.5 = NORMSINV(NORMSD, 'D8');
COMPUTE DSIZE/D12 = NORMSI * STDEV + MEAN;
BY PRODUCT_ID NOPRINT
END

A saída mostra que NORMSINV é o inverso de NORMSDST e mostra os valores originais:

Size              Z         NORMSD         NORMSI            DSIZE
----              -         ------         ------            -----
  16        -.07298         .47091        -.07298               16
  12        -.80273         .21106        -.80273               12
  12        -.80273         .21106        -.80273               12
  20         .65678         .74434         .65678               20
  24        1.38654         .91721        1.38654               24
  20         .65678         .74434         .65678               20
  24        1.38654         .91721        1.38654               24
  16        -.07298         .47091        -.07298               16
  12        -.80273         .21106        -.80273               12
   8       -1.53249         .06270       -1.53249                8
Information Builders