Comment : Référence : |
La fonction NORMSDST effectue des calculs sur la courbe de distribution normale standard, en calculant le pourcentage des valeurs de données qui sont inférieures ou égales à la valeur normalisée. Une valeur normalisée et un point sur l'axe des abscisses d'une courbe de distribution normale standards dans les déviations standard de moyenne. Ceci s'avère utile pour déterminer les centiles dans des données distribuées normalement.
La fonction NORMSINV est l'inverse de NORMSDST. Pour plus d'informations sur NORMSINV, consultez NORMSINV : Calculer la distribution normale cumulative inverse.
Les résultats de NORMSDST sont renvoyées en double précision avec une précision sur six chiffres significatifs.
Une courbe de distribution normale standard est une distribution normale ayant une moyenne égale à 0 et une déviation standard égal à 1. L'aire totale sous cette courbe est égale à 1. Un point sur l'axe des abscisses de la distribution normale standard est appelée une valeur normalisée. En supposant que vos données sont distribuées normalement, vous pouvez convertir un point de données en une valeur normalisée pour trouver le pourcentage des scores qui sont égaux ou inférieurs au score brut.
Vous pouvez convertir une valeur (score brut) à partir de vos données distribuées normalement en valeur normalisée équivalente (score-z) en procédant de la manière suivante :
z = (raw_score - mean)/standard_deviation
Pour convertir un score z en un score brut, utiliser la formule suivante :
raw_score = z * standard_deviation + mean
La moyenne des points de données xi, où i est entre 1 et n est :
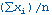
La déviation standard des points de données xi, où i est entre 1 et n est :

Le diagramme suivant illustre les résultats des fonctions NORMSDST et NORMSINV.
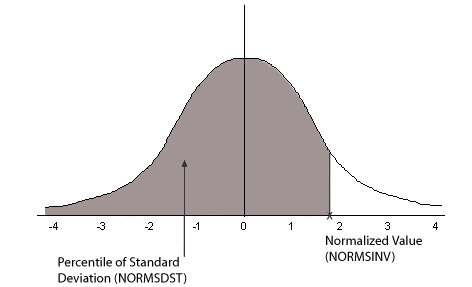
La plupart des mesures communes sont distribuées normalement. Le tracé de valeurs de données distribuées normalement ressemble à une courbe en forme de cloche. Les deux mesures requises pour décrire toute distribution normale sans la moyenne et la déviation standard :
- La moyenne est le point situé au centre de la courbe.
- La déviation standard décrit la répartition de la courbe. Il s'agit de la distance entre la moyenne et le point d'inflexion (où la courbe change de direction).
NORMSDST(value, 'D8');où :
- value
Une valeur normalisée.
- D8
Le format requis du résultat. La valeur renvoyée est au format double précision. Elle peut être attribuée à tout champ de format numérique valide.
NORMSDST calcule la valeur Z et trouve le centile correspondant :
DEFINE FILE GGPRODS
-* CONVERT SIZE FIELD TO DOUBLE PRECISION
X/D12.5 = SIZE;
END
TABLE FILE GGPRODS
SUM X NOPRINT CNT.X NOPRINT
-* CALCULATE MEAN AND STANDARD DEVIATION
COMPUTE NUM/D12.5 = CNT.X; NOPRINT
COMPUTE MEAN/D12.5 = AVE.X; NOPRINT
COMPUTE VARIANCE/D12.5 = ((NUM*ASQ.X) - (X*X/NUM))/(NUM-1); NOPRINT
COMPUTE STDEV/D12.5 = SQRT(VARIANCE); NOPRINT
PRINT SIZE X NOPRINT
-* COMPUTE NORMALIZED VALUES AND USE AS INPUT TO NORMSDST FUNCTION
COMPUTE Z/D12.5 = (X - MEAN)/STDEV;
COMPUTE NORMSD/D12.5 = NORMSDST(Z, 'D8');
BY PRODUCT_ID NOPRINT
ENDLa sortie est :
Size Z NORMSD ---- - ------ 16 -.07298 .47091 12 -.80273 .21106 12 -.80273 .21106 20 .65678 .74434 24 1.38654 .91721 20 .65678 .74434 24 1.38654 .91721 16 -.07298 .47091 12 -.80273 .21106 8 -1.53249 .06270